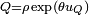Quaternion - Définition

Propriétés mathématiques

Classification algébrique

Le théorème de Frobenius généralisé montre que les extensions du corps des réels sont peu nombreuses. De fait, il n'en existe que quatre : le corps des réels lui-même, celui des nombres des complexes , celui des quaternions et celui des octonions . Le corps des quaternions n'est pas commutatif et celui des octonions n'est pas associatif. Dans ce contexte, les quaternions peuvent être définis comme le plus petit corps non-commutatif contenant .

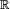
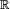
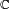
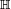
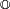
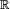
Dans le même ordre d'idée, le théorème de Hurwitz (1898) montre que les algèbres de composition sur un corps K, c'est-à-dire les algèbres munies d'une norme non-dégénérée, sont de dimensions 1, 2, 4 ou 8. Ces algèbres peuvent être obtenues à partir de la construction de Cayley-Dickson (en). De plus

• les algèbres de composition de dimension 1 n'existent que lorsque char(K) ≠ 2.
• les algèbres de composition de dimension 1 et 2 sont commutatives et associatives.
• les algèbres de composition de dimension 2 sont ou bien des extensions quadratiques de K, ou bien isomorphes à .
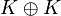
• les algèbres de composition de dimension 4 sont des algèbres de quaternions. Elles sont associatives mais pas commutatives.
• les algèbres de composition de dimension 8 sont des algèbres d'octonions. Elles ne sont ni associatives, ni commutatives.

Sous-ensembles particuliers

Racines carrées

Le corps des quaternions n'étant pas commutatif, un polynôme peut avoir plus de racines distinctes que son degré.

Considérons par exemple, le polynôme , où dont les racines sont les racines carrées du nombre réel λ. En écrivant , elle devient . La partie vectorielle de ce carré étant nulle, on doit avoir , c'est-à-dire, soit , auquel cas , soit , auquel cas , ce qui montre que les racines carrées d'un nombre réel négatif sont situées sur une sphère dans l'espace R³.

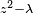
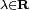
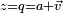
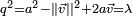
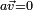
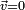
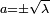
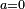
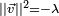
Pour trouver les racines d'un quaternion général , écrivons sa racine sous sa forme polaire , avec, avec . Un calcul immédiat donne . D'où on déduit successivement , au signe près; puis de , à près; puis .

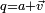
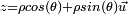
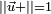
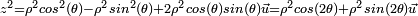
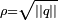
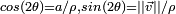
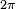
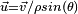
On est donc dans l'un des cas suivants:

• La racine carrée de est 0 ;
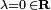
• Les racines carrées d'un réel négatif sont les vecteurs de la sphère d'équation ;
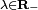
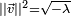
• Un quaternion qui n'est pas un réel négatif, possède deux racines carrées opposées.

Sous-algèbres

Pour un quaternion non réel avec , on peut écrire . Donc et, par récurrence, . Ceci montre que la sous-algèbre engendrée par un quaternion q non réel est . C'est aussi la sous-algèbre engendrée . Or ce dernier élément est tel que . La sous-algèbre est donc isomorphe au plan complexe C.

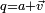
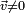
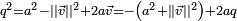
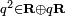
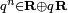
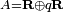
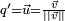
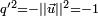
Si une sous-algèbre A contient deux quaternions et , alors elle contient aussi le quaternion . Donc, si et ne sont pas colinéaires, A contient tout l'espace R³, et, par suite, A = H.

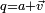
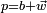
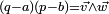
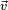
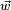
En résumé, les sous-algèbres de H sont

• Les sous-algèbres triviales R et H ;
• Une infinité de plans isomorphes au corps des complexe C, l'image de i pouvant être pris comme n'importe quel élément arbitraire de la sphère S des quaternions unitaires purs.

Quaternions unitaires et forme polaire

Quaternions unitaires

Les quaternions unitaires sont, par définition, les quaternions de norme 1. Leur ensemble est topologiquement isomorphe à la sphère S.

Un quaternion est unitaire si, et seulement si, , de sorte que la restriction du produit de Hamilton aux quaternions unitaires fait de la sphère unitaire un groupe multiplicatif. Nous verrons plus loin que ce groupe agit par rotation sur l'espace tridimensionnel des quaternions purs.

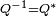
Ils forment une sphère, et nous verrons qu'on peut établir une sorte de correspondance entre un quaternion unitaire et une rotation vectorielle dans l'espace euclidien de dimension 3, et que cette particularité permet une représentation simple du produit de deux rotations vectorielles.

Versors

Pour tout quaternion Q, le quaternion est un quaternion unitaire, appelé versor (ou verseur) de Q.

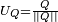
Tout quaternion apparait donc comme le produit d'un nombre réel positif par un quaternion unitaire.

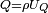
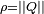
On remarquera que et que .

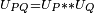
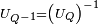
Par ailleurs, , d'où on déduit que .

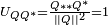
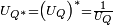
Forme polaire

On peut poursuivre plus loin la décomposition précédente. En effet, de , pour un quaternion unitaire , on tire l'existence d'un réel , tel que et où est un vecteur unitaire de R³.

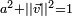
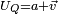
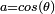
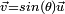
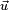
Finalement, tout quaternion s'écrit sous la forme , où est un réel positif et u_Q est un quaternion unitaire de composante réelle nulle, représenté par , vecteur de la sphère R³. Si Q est non réel, cette décomposition est unique, à près pour θ ; si Q est réel, le choix de est arbitraire.

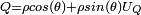
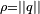
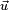
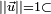
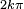
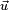
Il est possible de définir (par la série usuelle) une fonction exponentielle dans les quaternions, et l'on montre qu'avec les notations précédentes, on a .