Quaternion - Définition
La liste des auteurs de cet article est disponible ici.
Composition de rotations vectorielles et produit de quaternions
La propriété précédente justifie le fait que l'on a coutume de dire, mais de façon peu rigoureuse, que le quaternion
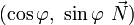
En utilisant le même langage approximatif, on peut dire que la composition de deux rotations successives
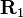
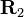
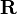
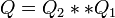
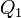
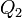
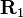
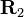
Montrons-le :
En posant :
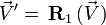
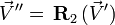
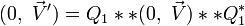
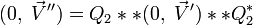
![(0,\ \vec V'') = Q_2 ** \left[Q_1 ** (0,\ \vec V) ** Q^*_1\right] ** Q^*_2](https://static.techno-science.net/illustration/Definitions/autres/8/8299145d2c1ffa2330e587310d8327c4_02d57fd4319c5d97a326414c76b85eb7.png)
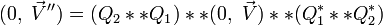
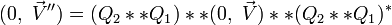
Ce qui établit la propriété annoncée pour la composition de deux rotations et que nous écrirons :
![\Bigg(0,\ \mathbf R_{\left[2\varphi_2, \vec N_2\right]}\left(\mathrm R_{\left[2\varphi_1, \vec N_1\right]} (\vec V)\right)\Bigg) = (\cos \varphi_2,\ \sin \varphi_2\ \vec N_2) ** (\cos \varphi_1,\ \sin \varphi_1\ \vec N_1) ** (0,\ \vec V) ** (\cos \varphi_1,\ -\sin \varphi_1\ \vec N_1) ** (\cos \varphi_2,\ -\sin \varphi_2\ \vec N_2)](https://static.techno-science.net/illustration/Definitions/autres/b/b0cb3043a7a88fcb6ab461b5330799d2_b9b2f2d073712b2272676814b71f765b.png)
Applications
Alors qu'ils peuvent être utiles en dimension 3, les quaternions ne sont pas employés dans d'autres dimensions (bien que des extensions comme celles des biquaternions et des algèbres de Clifford soient en théorie utilisables). En effet, la notion de vecteur a presque universellement remplacé celle des quaternions en science et en technologie au milieu du XXe siècle.
Aujourd'hui, les quaternions redeviennent plus populaires et trouvent leur place en infographie, en théorie de la commande, dans le traitement du signal, dans la commande de mouvement et la mécanique orbitale, principalement pour représenter les rotations et les orientations en dimension 3. Par exemple, il est fréquent que les systèmes de commande de déplacement d'un vaisseau spatial soient régis en termes de quaternions. La raison est qu'effectuer beaucoup d'opérations sur les quaternions est numériquement plus stable que d'effectuer beaucoup d'opérations sur les matrices.
Interpolation de rotations
Si l'on prend deux rotations de l'espace ra et rb, l'interpolation linéaire de ces rotations n'est en général pas une rotation. Pour pouvoir interpoler, il faut soit
- utiliser les angles d'Euler,
- utiliser les quaternions.
Dans le dernier cas, les 2 rotations sont représentées par 2 quaternions qa et qb sur la sphère unité S3, et l'interpolation correspond à la géodésique entre ces 2 points

















































