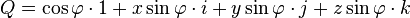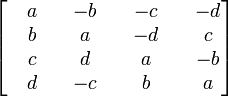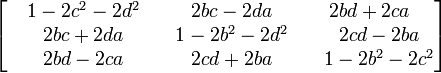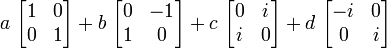Quaternion - Définition
La liste des auteurs de cet article est disponible ici.
La notation (a, V)
Le quaternion
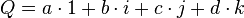

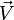
On écrit :
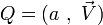
Cette notation permet de définir la somme et le produit de la façon suivante :
|
|
Elle permet aussi de re-définir ou définir les 3 notions suivantes :
- le conjugué
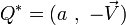
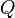
- le produit scalaire de deux quaternions :
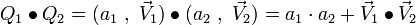
d'où l'on déduit :
- la norme d'un quaternion :
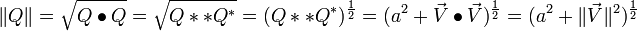
nota :
Soit à présent un quaternion
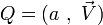
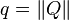
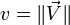
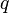
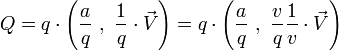
Or
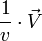
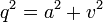
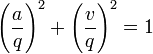
Il en résulte qu'il existe :
- un angle
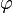


- un vecteur normé
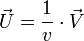
qui sont tels que l'on puisse écrire le quaternion
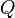
|
|
Cette façon d'écrire un quaternion est importante : les termes du couple,
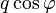
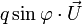
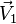
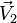
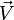
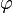

Correspondance entre quaternion unitaire et rotation vectorielle
On peut démontrer que le transformé
![\vec V' = \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V) \,](https://static.techno-science.net/illustration/Definitions/autres/5/5d416c2b9af7eb7a1b168bfcc1b35300_c7ea6e63c364e21d14b630f7315e4230.png)
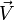
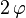
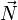
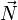
|
|
où
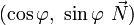
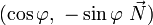
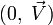
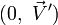
On peut aussi écrire cette transformation avec la notation
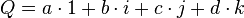
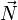
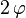
|
|
Double produit de quaternions
De même que l'on peut calculer un double produit vectoriel, il est possible de calculer un double produit de quaternions.
Notations matricielles
De même qu'il est possible de mettre en correspondance le nombre complexe
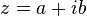
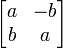
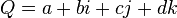
|
|
ou encore avec la matrice réelle suivante :
|
|
Il existe plusieurs représentations matricielles d'un quaternion. La matrice précédente en est une. Celle qui suit est plus souvent utilisée. Ainsi, la matrice réelle créée à partir d'un quaternion s'écrit de cette façon (en gardant q=a+ib+jc+kd):
Si le quaternion unitaire représente une rotation depuis l'origine, on peut le représenter à l'aide d'une matrice 3x3
|
|
Avec ces équivalences, la somme et le produit de deux quaternions correspondent respectivement à la somme et au produit des matrices qui leur correspondent.
Remarque :
La matrice complexe
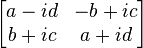
|
|
où les 4 matrices :
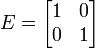
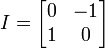
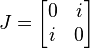
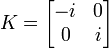
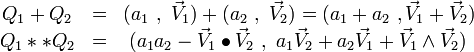
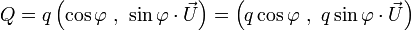
![(0,\ \vec V') = \left(0,\ \mathbf R_{\left[2\varphi, \vec N\right]}(\vec V)\right) = (\cos \varphi,\ \sin \varphi\ \vec N) ** (0,\ \vec V) ** (\cos \varphi,\ -\sin \varphi\ \vec N)](https://static.techno-science.net/illustration/Definitions/autres/6/6e790fda1d339c81a12401795874c2c7_9b57d3a6c1056839f4e5bbda837a4b2d.png)