Quaternion - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un quaternion est un type de nombre hypercomplexe. L'ensemble des quaternions, noté


Les quaternions furent mis en forme au XIXe siècle, par Hamilton qui cherchait à construire un ensemble de nombres ayant, dans l'espace, des propriétés analogues à celles que possèdent les nombres complexes dans le plan. Il les présente comme des quadruplets de réels.
L'ensemble des quaternions peut être muni d'une addition et d'une multiplication qui font de lui un des premiers exemples de corps non commutatif.
La relation qui existe entre les quaternions et les rotations en dimension 3 fait de l'ensemble des quaternions un outil utile pour le traitement de l'espace comme en infographie ou en théorie de la commande.
Origines et principes
Histoire
Les quaternions furent « découverts » par William Rowan Hamilton en 1843 à partir des travaux de Leonhard Euler et, au siècle suivant, Carl Friedrich Gauss. Il étudiait alors l'interprétation géométrique de l'arithmétique de nombres complexes dans le plan et cherchait à obtenir des résultats analogues dans l'espace à trois dimensions.
Après des années de recherches sur la construction d'une algèbre avec des « triplets » de trois nombres réels, il butait sur la multiplication, et en particulier la conservation des normes (Georg Ferdinand Frobenius a démontré en 1877 qu'une telle multiplication de triplets était impossible à définir).
Il eut alors l'idée d'utiliser des « quadruplets » en employant une dimension supplémentaire. Selon ses dires, il marchait, le 16 octobre 1843, le long du canal royal, avec son épouse quand soudain lui vint à l'esprit la solution sous la forme des relations : i2 = j2 = k2 = ijk = − 1. Il grava alors promptement ces relations avec un couteau dans une pierre du pont de Brougham (maintenant appelé Broom Bridge) à Dublin. Cette inscription, malheureusement effacée par le temps, a été remplacée par une plaque à la mémoire de Sir William Rowan Hamilton.
La théorie a été généralisée et d'autres ensembles comme les octonions ont été découverts par la suite. Un élément d'un ensemble de cette nature fut qualifiée de nombre hypercomplexe jusqu'à la Première Guerre mondiale. Ces ensembles sont maintenant considérés comme des exemples d'algèbres semi-simples. Le théorème d'Artin-Wedderburn fournit une méthode de construction générique et se fonde sur la théorie des représentations d'un groupe fini. La construction des quaternions est donnée dans l'article représentations du groupe des quaternions. Elle correspond à l'unique algèbre simple fidèle de la représentation du groupe de quaternions sur le corps des nombres réels.
Principe
Hamilton décrivit un quaternion comme un quadruplet de nombres réels, le premier élément étant un « scalaire », et les trois éléments restants formant un « vecteur », ou « imaginaire pur ».
Il put ainsi définir une multiplication avec les bonnes propriétés. Celle-ci peut se résumer à cette table de multiplication :
| · | 1 | i | j | k |
| 1 | 1 | i | j | k |
| i | i | -1 | k | -j |
| j | j | -k | -1 | i |
| k | k | j | -i | -1 |
Tout quaternion H peut être considéré comme une combinaison linéaire des quatre quaternions "unités" 1, i, j, et k :
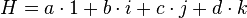
(où a, b, c, d sont des nombres réels).
H peut également s'écrire: H = z + z'·j (avec z et z' des nombres complexes de la forme a + b·i)
Les nombres réels a, b, c et d sont caractéristiques de H : il n'existe qu'une seule façon d'écrire H sous cette forme, et tout quaternion comportant ces mêmes 4 caractéristiques est nécessairement égal à H (la réciproque est vraie).
a s'appelle la composante réelle ou scalaire de H, tandis que b, c et d sont les composantes complexes de H. On dit aussi que a est le scalaire de H et que le triplet {b, c, d} ou [
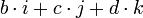
Cette découverte entraîna l'abandon de l'utilisation exclusive des lois commutatives, une avancée radicale pour l'époque. Les vecteurs et les matrices faisaient encore partie du futur, mais Hamilton venait en quelque sorte d'introduire le produit vectoriel et le produit scalaire des vecteurs.
Non-commutativité
L'algèbre des quaternions n'est plus commutative, mais partiellement anticommutative : 1 · i = i · 1 = i mais i · j = k et j · i = -k.
| Cette non commutativité est d'ailleurs tout à fait compatible avec une interprétation géométrique des quaternions, par exemple les rotations vectorielles du plan sont commutatives, mais celles de l'espace ne le sont pas :
|

















































