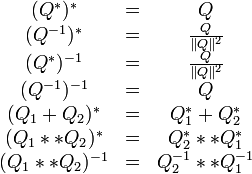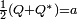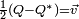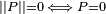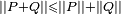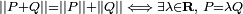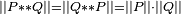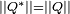Quaternion - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Origines et principes - Définition - Propriétés mathématiques - Sous-ensembles particuliers - Quaternions unitaires et forme polaire - Les similitudes de l'espace et les quaternions - La notation (a, V) - Correspondance entre quaternion unitaire et rotation vectorielle - Double produit de quaternions - Notations matricielles - Composition de rotations vectorielles et produit de quaternions - Applications

Définition

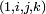
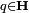
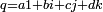
L'espace vectoriel des quaternions H sur le corps des réels est un espace vectoriel réel de dimension quatre rapporté à une base notée $\scriptstyle (1, i, j, k)$ . Tout quaternion $\scriptstyle q \in \mathbf H$ , s'écrit donc de manière unique $\scriptstyle q = a 1 + b i + c j + d k$ .

Scalaires et vecteurs

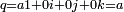
L'ensemble des quaternions de la forme $\scriptstyle q = a 1 + 0 i + 0 j + 0 k = a$ s'identifie aux nombres réels. Ils sont appelés scalaires ou réels.

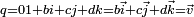
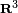
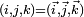
Les quaternions de la forme $\scriptstyle q = 0 1 + b i + c j + d k = b \vec i + c \vec j + d \vec k = \vec v$ , forment un espace vectoriel tridimensionnel, identifié à $\scriptstyle \mathbf R ^3$ , par identification des bases $\scriptstyle (i, j, k) = (\vec i, \vec j, \vec k)$ . On les appelle quaternions purs, quaternions vectoriels, ou par abus de langage, vecteurs.

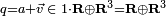
Tout quaternion $q$ se décompose en une somme d'un réel et d'un vecteur $\scriptstyle q = a + \vec v \; \in \; 1 \cdot \mathbf R \oplus \mathbf R ^3 = \mathbf R \oplus \mathbf R ^3$ , appelées partie scalaire (ou réelle) et partie vectorielle de $q$ . Cette décomposition est unique.

Addition

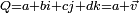
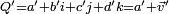
La somme de deux quaternions $\scriptstyle Q = a + b i + c j + d k = a + \vec v$ et $\scriptstyle Q' = a'+ b'i + c'j + d'k = a' + \vec v'$ , est définie composant par composant par:

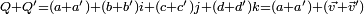
Cette addition fait de H un groupe abélien(commutatif) par transport de structure.

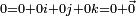
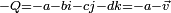
Son élément neutre est $\scriptstyle 0 = 0 + 0i + 0j + 0k = 0 + \vec 0$ et l'opposé d'un quaternion $\scriptstyle -Q = -a -bi -cj -dk = -a - \vec v$ s'obtient en inversant les signes de ses composants.

Multiplication de Hamilton

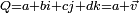
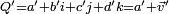
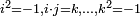
Le produit de deux quaternions $\scriptstyle Q = a + b i + c j + d k = a + \vec v$ et $\scriptstyle Q' = a' + b' i + c' j + d' k = a' + \vec v'$ , s'obtient en développant le produit formellement, puis en effectuant les réductions $\scriptstyle i^2 = -1, i\cdot j = k, ..., k^2 = -1$ définies par la table de multiplication donnée plus haut. Il est commode, pour la distinguer de la multiplication des réels, de représenter la multiplication des quaternions par $* *$ (une double étoile).

Tous calculs faits, on obtient

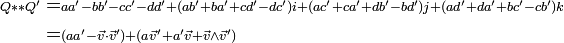
Dans cette dernière formule le $\scriptstyle \cdot$ désigne le produit scalaire et $\scriptstyle \wedge$ le produit vectoriel des composantes vectorielles des deux quaternions.

Cette multiplication fait de H un anneau associatif unitaire, la distributivité résultant de la bilinéarité des produits scalaires et vectoriels.

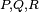
Pour tout quaternion $\scriptstyle P, Q, R$ , on a :

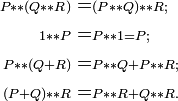
\begin{align}\scriptstyle P**(Q**R) &= \scriptstyle (P**Q)**R ; \\ \scriptstyle 1 ** P &= \scriptstyle P ** 1 = \scriptstyle P ; \\ \scriptstyle P**(Q+R)&= \scriptstyle P**Q+P**R ; \\ \scriptstyle (P+Q)**R &= \scriptstyle P**R+Q**R . \end{align}

Non-commutativité

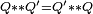
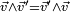
La multiplication n'est pas commutative. De fait, la formule précédente montre que pour que $\scriptstyle Q ** Q' = Q' ** Q$ , il faut et il suffit que $\scriptstyle \vec v \wedge \vec v' = \vec v' \wedge \vec v$ , c'est-à-dire que leurs composantes vectorielles soient colinéaires.

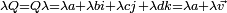
En particulier, un quaternion commute à tous les quaternions si, et seulement si, sa partie vectorielle est nulle, c'est-à-dire s'il est réel. Pour , la formule $\scriptstyle \lambda Q = Q \lambda = \lambda a + \lambda bi + \lambda cj + \lambda dk = \lambda a+ \lambda \vec v$ , définit alors une multiplication externe qui munit H d'une structure d'espace vectoriel. Cette opération préserve le sous-espace des scalaires R et des vecteurs R³. Sur ces sous-espaces, elle coïncide avec les multiplications habituelles.

En résumé:

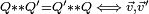
$\scriptstyle Q ** Q' = Q' ** Q \iff \vec v, \vec v'$ colinéaires
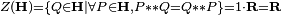
$\scriptstyle Z(\mathbf H) = \{ Q \in \mathbf H | \forall P \in \mathbf H , P ** Q = Q ** P \} = 1 \cdot \mathbf R = \mathbf R$

Conjugaison, norme, inversion

Les quaternions sont munis d'une conjugaison, qui est un anti-morphisme involutif, qui permet de définir une norme, puis l'inverse d'un quaternion. On vérifie alors que H est un corps.

Conjugaison

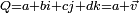
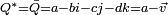
Le conjugué du quaternion $\scriptstyle Q = a + b i + c j + d k = a + \vec v$ est le quaternion obtenu en conservant sa partie scalaire et en prenant l'opposé de sa partie vectorielle $\scriptstyle Q^* = \bar Q = a - b i - c j - d k = a -\vec v$ .

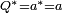
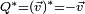
On remarquera que le conjugué d'un scalaire $\scriptstyle Q^* = {a}^* = a$ est lui-même et que le conjugué d'un vecteur pur $\scriptstyle Q^* = {\left( \vec v \right)}^* = -\vec v$ est son opposé. Pour cette raison Hamilton se référait à la conjugaison comme inverse spatial.

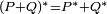
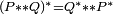
La conjugaison est linéaire, i.e. $\scriptstyle (P+Q)^* = P^*+Q^*$ , et un anti-morphisme, inversant le sens du produit $\scriptstyle (P ** Q)^* = Q^* ** P^*$

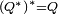
C'est une involution, égale à son propre inverse $\scriptstyle {(Q^*)}^* = Q$ .

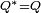
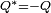
Les invariants, tels que $\scriptstyle Q^* = Q$ , sont les réels et les anti-invariants, tels que $\scriptstyle Q^* = -Q$ , sont les quaternions purs.

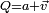
La conjugaison permet de retrouver facilement la partie réelle et vectorielle d'un quaternion $\scriptstyle Q = a + \vec v$ :

$\scriptstyle \frac 1 2 (Q+Q^*) = a$
$\scriptstyle \frac 1 2 (Q-Q^*) = \vec v$

Norme

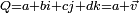
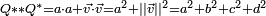
Le produit d'un quaternion $\scriptstyle Q = a + bi + cj + dk = a + \vec v$ par son conjugué $Q *$ donne $\scriptstyle Q ** Q^* = a \cdot a + \vec v \cdot \vec v = a^2 + \left|| \vec v \right||^2 = a^2 + b^2 + c^2 + d^2$ qui est un nombre réel positif.

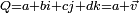
On appelle norme du quaternion $\scriptstyle Q = a + bi + cj + dk = a + \vec v$ , le nombre réel positif

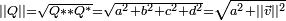
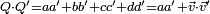
Cette norme dérive du produit scalaire canonique sur R⁴, défini par $\scriptstyle Q \cdot Q' = aa' + bb' + cc' + dd' = aa' + \vec v \cdot \vec v'$ . Elle coïncide avec la norme euclidienne dans l'espace quadri-dimensionnel R⁴, sa restriction aux scalaires avec la valeur-absolue et sa restriction aux vecteurs avec la norme usuelle dans l'espace tridimensionnel standard.

On a :

$\scriptstyle \left|| P \right|| = 0 \iff P = 0$
$\scriptstyle \left|| P+Q \right|| \leqslant \left|| P \right|| + \left|| Q \right||$
$\scriptstyle \left|| P+Q \right|| = \left|| P \right|| + \left|| Q \right|| \iff \exists \lambda \in \mathbf R, \; P = \lambda Q$
$\scriptstyle \left|| P ** Q \right|| = \scriptstyle \left|| Q ** P \right|| = \left|| P \right|| \cdot \left|| Q \right||$
$\scriptstyle \left|| Q^* \right|| = \left|| Q \right||$

Inverses et divisions

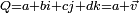
Si un quaternion $\scriptstyle Q = a + bi + cj + dk = a + \vec v$ n'est pas nul, il possède un unique inverse

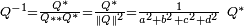
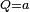
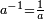
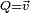
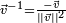
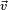
Si $\scriptstyle Q = a$ est réel, son inverse $\scriptstyle a^{-1} = \frac 1 a$ est l'inverse de a en tant que réel. Et si $\scriptstyle Q = \vec v$ est un vecteur, son inverse $\scriptstyle {\vec v}^{-1} = \frac {- \vec v} {{\left|| \vec v \right|| }^2}$ est le vecteur pointant dans la direction opposée à $\scriptstyle \vec v$ et de norme inverse.

La multiplication n'étant pas commutative, on peut définir la division du quaternion $\scriptstyle P$ par le quaternion (non nul) $\scriptstyle Q$ de deux façons différentes :

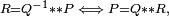
la division à gauche $\scriptstyle R = Q^{-1} ** P \iff P = Q ** R,$
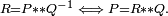
la division à droite $\scriptstyle R = P ** Q^{-1} \iff P = R ** Q.$

Conjugué d'un inverse, conjugué de la somme et du produit de deux quaternions

On montre aisément les égalités :

\begin{matrix}(Q^*)^* &=& Q\\(Q^{-1})^* &=& \frac{Q}{\|Q\|^2}\\(Q^*)^{-1} &=& \frac{Q}{\|Q\|^2}\\(Q^{-1})^{-1} &=& Q\\(Q_1 + Q_2)^* &=& Q^*_1 + Q^*_2\\(Q_1 ** Q_2)^* &=& Q^*_2 ** Q^*_1\\(Q_1 ** Q_2)^{-1} &=& Q^{-1}_2 ** Q^{-1}_1\end{matrix}\,

Origines et principes

Propriétés mathématiques

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Page générée en 0.137 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise