Quaternion - Définition

Les similitudes de l'espace et les quaternions

Pour démystifier les quaternions, nous allons faire un petit détour instructif par la géométrie élémentaire et en particulier par les similitudes dans l'espace. Une similitude dans est entièrement définie par la triple donnée :

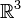
• d'un axe de rotation bien orienté (un vecteur unitaire U),
• d'un angle 2φ défini à 2kπ près et
• d'un rapport d'homothétie k, un réel strictement positif.
  L'effet d'une similitude sur tous les vecteurs peut être considéré grossièrement comme un vissage avec expansion.

Voyage et trajets

Plus précisément, l'image du transformé d'un vecteur V (dont l'origine est supposée située sur l'axe U) est obtenue d'abord par une multiplication (homothétie) de ce vecteur par k, suivi par une rotation d'angle 2φ autour de l'axe de rotation (on pourrait aussi commencer par la rotation et la faire suivre de l'homothétie, mais il faudrait modifier un peu les explications qui vont suivre...). Cette rotation fait tourner d'un angle 2φ l'extrémité du vecteur kV sur un cercle (C) centré sur l'axe et situé dans un plan perpendiculaire à U. Or sur ce cercle, il y a deux façons d'effectuer le trajet : soit en utilisant un arc, soit en utilisant son complémentaire, ces arcs ne pouvant pas malheureusement être distingués par la seule mesure 2φ + 2kπ.
C'est précisément cette difficulté que permet de résoudre la notion de quaternion. Schématiquement, on peut dire qu'un quaternion, c'est comme une similitude qui saurait distinguer les 2 trajets que peut emprunter la rotation associée.

Dans la vie courante, si pour un voyage entre deux localités L et L, vous avez a priori deux trajets possibles, la distinction entre ces trajets peut être faite en désignant deux sites-étapes intermédiaires s et s. Et en parlant du trajet s et du trajet s, vous sous-entendrez les localités de départ et d'arrivée L et L.

En conservant cette analogie, il nous faut donc définir deux points intermédiaires sur les deux arcs du trajet.

À mi-chemin

Les points situés à mi-chemin sont parfaits pour cette mission. En effet, si je divise l'angle de vecteurs 2φ + 2kπ par 2, j'obtiens deux angles distincts φ + 2kπ et φ-π + 2kπ. Or, si j'utilise la rotation d'axe U et d'angle φ + 2kπ, je définis un site-étape différent de celui que j'obtiens avec la rotation φ-π + 2kπ. Ainsi à la similitude sim(U, 2φ, k), il correspond deux trajets distincts qui sont représentés par les deux quaternions distincts quat(U, φ, k) et quat(U, −π+φ, k).

Le formalisme

Le triplet (U, φ, k) peut s'écrire de façon équivalente sous la forme du couple (kcos(φ), ksin(φ)∙U) de la notation . Et en utilisant des vecteurs a et b orthogonaux à U convenables, il est facile de montrer que ce couple prend la forme (a.b, a^b). Ainsi, nos sites-étapes nous permettent de revenir à des opérations très simples sur des vecteurs. Et comme ces opérations sont riches de propriétés remarquables, on sait définir (comme on l'a vu ci-dessus) une multiplication et une addition des quaternions. Vous pouvez « voir » ces deux opérations sur les quaternions ici : http://www.alcys.com

Une voie de recherche prometteuse peut être consultée sur le site [1]. On y définit justement la similitude dans l'espace à trois dimensions par un bivecteur qui est au couple de vecteurs ce que le vecteur est au couple de points. La loi de composition introduite dans ces bivecteurs est effectivement non commutative, et la restriction de cet ensemble au plan est l'ensemble des complexes.