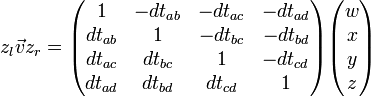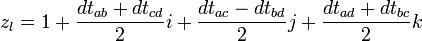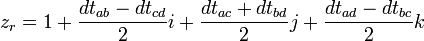Quaternions et rotation dans l'espace - Définition

Expliquer les propriétés des quaternions à l'aide des rotations

Non-commutativité

La multiplication des quaternions est non commutative. Comme multiplier des quaternions unitaires revient à composer les rotations dans l'espace à trois dimensions, on peut rendre cette propriété intuitive grâce au fait que les rotations en trois dimensions ne commutent pas en général.

Un simple exercice consistant à appliquer deux rotations successives à un objet asymétrique (par exemple un livre) peut l'expliquer. D'abord, tournez un livre de 90 degrés dans le sens des aiguilles d'une montre autour de l'axe des Z. Ensuite, basculez-le de 180 degrés autour de l'axe des X et mémorisez le résultat. Revenez à la position de départ, de manière à pouvoir lire à nouveau le titre du livre, et appliquez les rotations en ordre inverse. Comparez le résultat au résultat précédent. Cela montre que, en général, la composition de deux rotations différentes autour de deux axes distincts de l'espace ne commute pas.

Les quaternions sont-ils orientés ?

Il convient de remarquer que les quaternions, comme n'importe quelle rotation ou application linéaire, ne sont pas "orientés" (il n'y a pas de sens direct ou indirect). L'orientation d'un système de coordonnées provient de l'interprétation des nombres dans l'espace physique. Quelle que soit la convention d'orientation que l'on choisisse, faire tourner le vecteur X de 90 degrés autour du vecteur Z renverra le vecteur Y — la théorie et les calculs donnent le même résultat.

Les paires de quaternions unitaires comme rotations dans l'espace à 4 dimensions

Une paire de quaternions unitaires z_l et z_r peut représenter n'importe quelle rotation de l'espace en quatre dimensions. Étant donné un vecteur en quatre dimensions, considéré comme un quaternion, nous pouvons faire tourner ainsi :

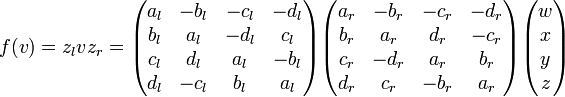
Les deux matrices vérifient  : chacune de ces deux matrics (et donc également la combinaison des deux) représente une rotation. On remarquera que comme , les deux matrices doivent commuter. Par conséquent, il y a deux sous-groupes commutant de l'ensemble des rotations de l'espace en quatre dimensions. Il y a six degrés de liberté pour une rotation quelconque de l'espace à 4 dimensions, chacune de ces deux matrices représente 3 de ces 6 degrés de liberté.

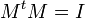
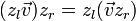
De la même façon qu'une rotation en quatre dimensions infinitésimale peut être représentée comme suit par une paire de quaternions, on peut représenter toutes les rotations de l'espace en 4 dimensions.