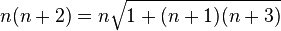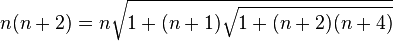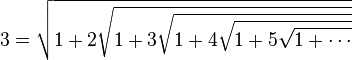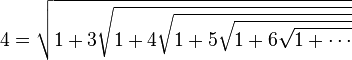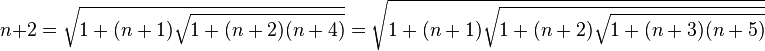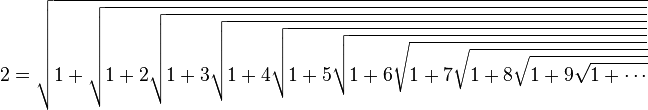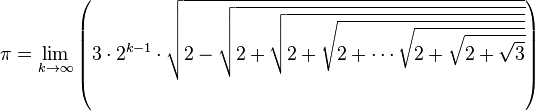Racine carrée - Définition
La liste des auteurs de cet article est disponible ici.
Curiosités
L’identité
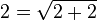
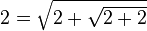
Pour des raisons analogues, on obtient :
-
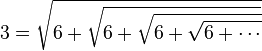
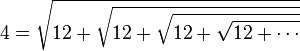
Si r est un entier strictement supérieur à 1,
Plus généralement, si p étant un nombre réel supérieur ou égal à 1,
Si p est égal à 1, on obtient le nombre d'or:
-
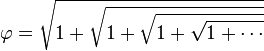
Le mathématicien Ramanujan obtint une formule alternative pour 3. Il partit de la décomposition
et construisit le produit n(n + p) en fixant p = 2
Il substitua le terme (n + 3)
Ramanujan réitéra à l’infini en remplaçant maintenant n par 1 et obtint la jolie formule :
(bien entendu, il doit ensuite démontrer que le passage à la limite est légal)
En fixant n et p à d’autres valeurs positives ou en élevant au carré une formule obtenue, on peut également construire d’autres belles formules comme :
En résumé, la relation suivante, itérée à l’infini :
permet donc d’exprimer tous les nombres entiers strictement supérieurs à 1 comme une itération infinie de racines carrées.
En particulier, en fixant n = 0
(toutes ces formules sont en fait des affirmations sur des limites, qui se démontrent, de manière assez délicate, par encadrements)
Le nombre π s’exprime sous la forme d’une itération infinie de racines carrées :
-
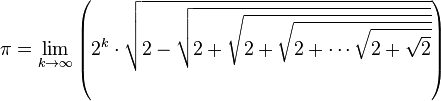
Ou encore :
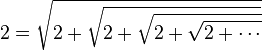
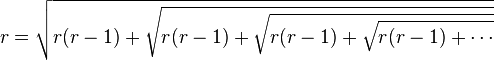
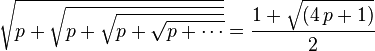
![(n+p)^2 = 1 + [n+(p-1)][n+(p+1)]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d2b6141735aa5e63c004c2334fdd055e_b38326805d6cbd75be8037b5b9dff57f.png)