Décomposition de Dunford - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la décomposition de Dunford s'inscrit dans la problématique de la réduction d'endomorphisme. Cette approche consiste à décomposer l'espace vectoriel en une somme directe de sous-espaces stables où l'expression de l'endomorphisme est plus simple.
Ce n'est pas une réduction dans le sens où elle n'est pas maximale. C'est-à-dire qu'il est parfois possible de pousser la décomposition en sous-espaces vectoriels stables plus petits.
Elle suppose comme hypothèses que l'espace vectoriel est de dimension finie et que le polynôme minimal est scindé, c'est-à-dire qu'il s'exprime comme produit de polynômes du premier degré. C'est toujours le cas si le corps est algébriquement clos, comme par exemple celui des nombres complexes. Dans le cas ou la propriété n'est pas vérifiée, alors il est possible d'étendre le corps à sa clôture algébrique, et l'espace vectoriel à ce nouveau corps et dans ce contexte d'appliquer la décomposition de Dunford. Le corps des nombres réels se voit par exemple très généralement étendre pour permettre une application de cette décomposition.
La décomposition de Dunford prouve que tout endomorphisme est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent, les deux endomorphismes commutant et étant uniques.
Cette décomposition est largement appliquée. Elle permet un calcul matriciel souvent rapide. C'est néanmoins souvent sous la forme de la réduction de Jordan qu'elle est utilisée.
Théorème
Le théorème de diagonalisabilité permet de déterminer la structure de u quand il admet un polynôme annulateur scindé à racines simples. La décomposition de Dunford s'applique à un cas plus général.
Théorème de la décomposition de Dunford — Soit u un endomorphisme d'un espace vectoriel E. Si u admet un polynôme minimal scindé, alors il peut s'écrire sous la forme u=d+n avec d un endomorphisme diagonalisable et n un endomorphisme nilpotent tels que d et n commutent (c'est-à-dire dn=nd). De plus d et n sont des polynômes en u et sont uniques.
Cas d'applications
En dimension finie le théorème de Cayley-Hamilton assure que χu(u) = 0 où χu désigne le polynôme caractéristique de u. Si χu est scindé alors u est décomposable.
C'est en particulier le cas pour tout endomorphisme d'un espace de dimension finie sur un corps algébriquement clos (
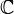
Démonstration
Via les sous-espaces caractéristiques
L'idée initiale de cette approche est donnée par la proposition suivante, démontrée dans l'article sur les polynômes d'endomorphismes dans le paragraphe sur les polynômes minimaux :
-
- Soit
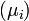
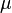
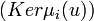
- Soit
Or, si le polynôme minimal est scindé, il peut s'écrire sous la forme:
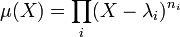
Si l'on note
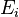
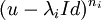
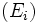
-
- L'espace E est somme directe de ces sous-espaces caractéristiques.
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stables par l'endomorphisme. La restriction de l'endomorphisme à
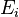
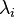
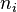
- La suite des
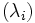
Ces considérations permettent de démontrer la décomposition de Dunford. Elle permettent de plus de démontrer les propriétés suivantes :
-
- Le polynôme minimal est le produit des polynômes de degré 1 et de racine les valeurs propres à la puissance l'indice de l'endomorphisme nilpotent associé.
-
- Le polynôme caractéristique est le produit des polynômes de degré 1 et de racines les valeurs propres à la puissance la dimension de l'espace caractéristique associé.
-
- Le déterminant est égal au produit des valeurs propres élevées à la puissance la dimension de l'espace caractéristique associé.
-
- La trace est égale à la somme des valeurs propres pondérées par les dimensions des espaces caractéristiques associés.
-
- L'espace E est somme directe de ces sous-espaces caractéristiques.
Le polynôme minimal est scindé, donc il s'écrit sous la forme de produits des éléments de la suite
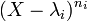
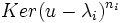
-
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stable par l'endomorphisme. La restriction de l'endomorphisme à
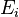
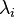
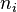
- Les sous-espaces caractéristiques sont non réduits au vecteur nul et stable par l'endomorphisme. La restriction de l'endomorphisme à
Considérons le polynôme
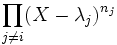
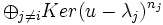
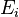
La restriction de u à
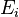
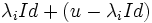
-
- La suite des
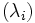
- La suite des
Montrons que
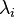
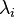
Considérons alors une valeur propre
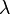
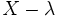
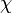
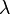
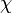
-
- L'endomorphisme u est la somme d'un endomorphisme diagonalisable et d'un endomorphisme nilpotent. Les deux endomorphismes commutent entre eux.
Considérons l'endomorphisme d sur E, qui pour tout vecteur
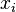
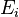
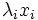
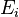
Considérons l'endomorphisme n sur E, qui pour tout vecteur
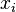
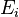
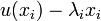
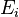
La somme d + n est égal à u et d et n commutent entre eux sur chaque espace caractéristique. La somme des espaces caractéristiques est égal à E. L'égalité et la commutativité sont donc vraies sur E.
-
- Le polynôme minimal est le produit des polynômes de degré 1 et de racines les valeurs propres à la puissance l'indice de l'endomorphisme nilpotent associé.
Il suffit de remarquer que
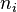
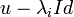
-
- Le polynôme caractéristique est le produit des polynômes de degré 1 et de racines les valeurs propres à la puissance la dimension de l'espace caractéristique associé.
Il suffit de calculer le polynôme caractéristique dans une base de Jordan.
-
- Le déterminant est égal au produit des valeurs propres élevées à la puissance de la dimension de l'espace caractéristique associé.
Il suffit de calculer le déterminant dans une base de Jordan.
-
- La trace est égale à la somme des valeurs propres multipliées par la dimension de l'espace caractéristique associé.
Il suffit de calculer la trace dans une base de Jordan.
Via les projecteurs
Un résultat notoire de l'approche par les polynômes d'endomorphismes réside dans le fait que la connaissance du polynôme minimal permet de définir une algorithmique fournissant à la fois les projecteurs sur les espaces caractéristiques mais aussi la composante diagonale et nilpotente de l'endomorphisme.
-
- La projection sur Ei parallèlement à la somme directe des autres espaces caractéristiques s'exprime comme un polynôme de l'endomorphisme u.
- La composante diagonale d de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
- La composante nilpotente n de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
-
- La projection sur Ei parallèlement à la somme directe des autres espaces caractéristiques s'exprime comme un polynôme de l'endomorphisme u.
C'est une conséquence directe de la dernière proposition du paragraphe sur les idéaux annulateurs. En effet, la famille des polynômes
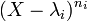
-
- La composante diagonale d de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
L'égalité suivante
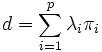
-
- La composante nilpotente n de l'endomorphisme u s'exprime comme un polynôme de l'endomorphisme u.
L'égalité suivante est vérifiée
![n=u-d=(X-P)[u]\,](https://static.techno-science.net/illustration/Definitions/autres/f/f1bddd0eb7de02080311faa6753e39cc_65a1fd0dae497410842f624aeadacd8e.png)

















































