Endomorphisme nilpotent - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un endomorphisme nilpotent est un morphisme d'un objet mathématique sur lui-même, qui, composé par lui-même un nombre suffisant de fois, donne le morphisme nul. C’est donc (lorsque les endomorphismes de cet objet forment un anneau) un élément nilpotent de cet anneau.
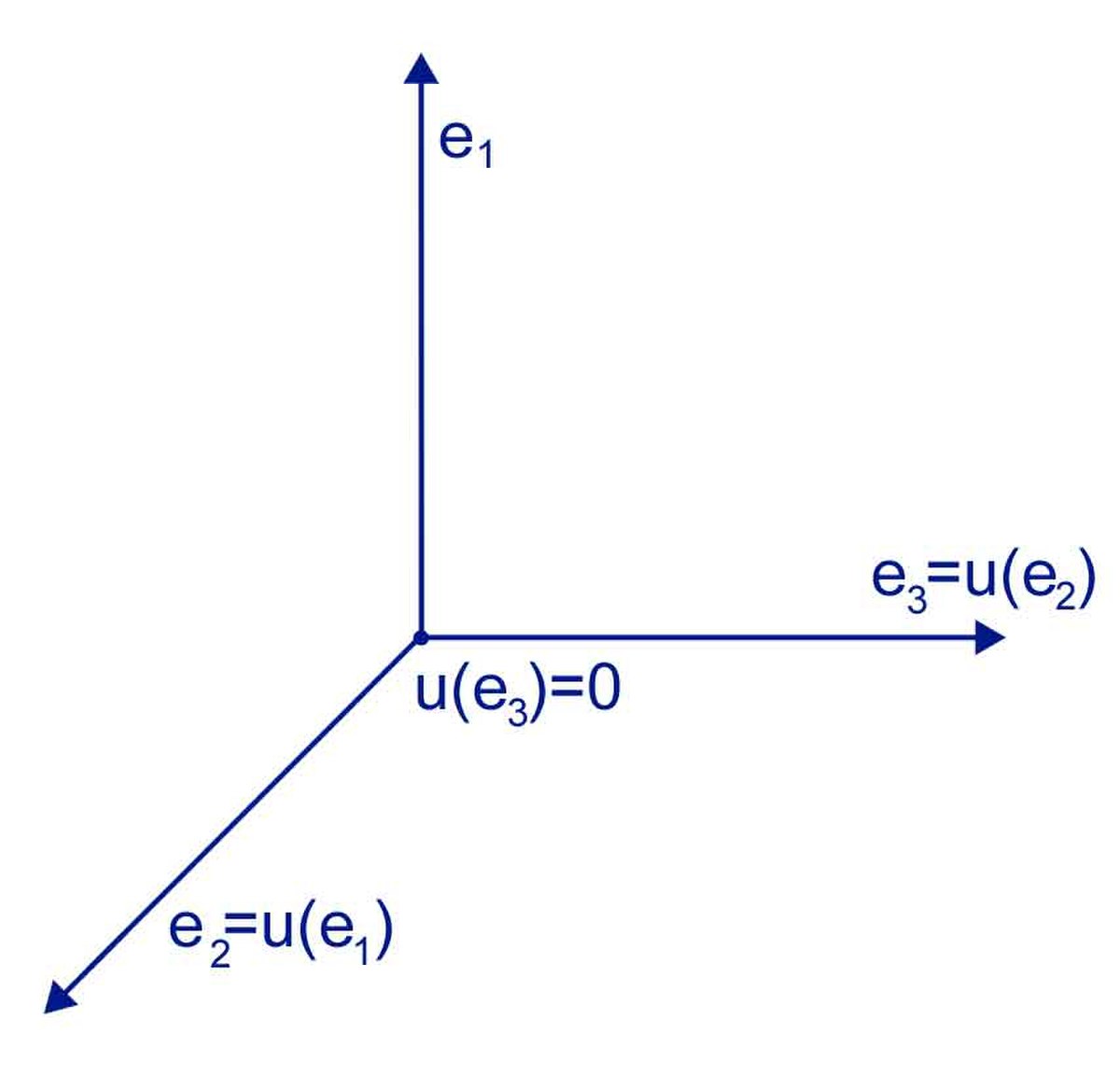
En algèbre linéaire, on considère les endomorphismes nilpotents d’un espace vectoriel. Un exemple est donné dans l'illustration. Ils interviennent dans la réduction des endomorphismes, c’est-à-dire la représentation d'un endomorphisme quelconque sous une forme la plus simple possible. Cette réduction sert par exemple pour la résolution d'équations différentielles linéaires.
On retrouve également le concept de nilpotence dans l'étude des groupe de Lie, avec l'analyse des algèbres de Lie nilpotentes.
Les endomorphismes nilpotents d'un espace vectoriel sont l'objet principal de cet article. Lorsque de plus cet espace est de dimension finie, chacun de ses endomorphismes est représenté par une matrice (dans une base de l'espace vectoriel concerné). L'endomorphisme est alors nilpotent si et seulement s'il a une matrice nilpotente, ce qui, par le calcul, permet une approche plus concrète du concept (toutes les propriétés générales des endomorphismes nilpotents ont leur pendant dans le contexte plus particulier des matrices nilpotentes), et offre d'importantes applications pratiques.
Définition
Soit E un espace vectoriel sur un corps K et u un endomorphisme de E. L'endomorphisme u est dit nilpotent si et seulement s'il existe un entier n>0 tel que un = 0. Le plus petit entier naturel n vérifiant cette propriété est alors appelé indice (de nilpotence) de l'endomorphisme u.
Soit x un vecteur de E, on appelle indice de x (pour l'endomorphisme nilpotent u) le plus petit entier naturel p tel que up(x) = 0.
Un sous-espace cyclique de E (pour l'endomorphisme nilpotent u) est un sous-espace vectoriel de E engendré par une famille de la forme (x, u(x), u2(x), ..., up-1(x)), où x est un vecteur d'indice p.
Propriétés
L'exemple illustre l'essentiel des propriétés des endomorphismes nilpotents. On y trouve des propriétés sur l'indice des endomorphismes et des vecteurs, des conditions nécessaires et suffisantes grâce aux polynômes. Des réductions avec une décomposition en espaces propres et l'existence d'une base réduite. Il existe aussi des propriétés calculatoires des matrices nilpotentes traitées dans l'article Matrice nilpotente.
Nilpotence et indice
L'indice d'un endomorphisme nilpotent possède deux grandes propriétés :
-
- L'indice d'un endomorphisme nilpotent est inférieur ou égal à la dimension de l'espace (pour la démonstration penser à utiliser la suite (kerfn)).
- Il existe un vecteur dont l'indice est celui de l'endomorphisme.
Nilpotence et polynômes en dimension finie
Les polynômes fournissent non seulement des conditions nécessaires et suffisantes pour la nilpotence, mais renseignent de plus sur l'indice.
-
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à ( − X)n ou n est la dimension de l'espace.
- Un endomorphisme est nilpotent si et seulement si son polynôme minimal est égal à Xp ou p est l'indice de l'endomorphisme.
- Le polynôme minimal d'un vecteur x est égal à
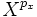
Nilpotence et réduction en dimension finie
Le principe de réduction consiste à trouver une décomposition en somme directe de sous-espaces stables de l'espace vectoriel. Il en existe une pour les endomorphismes nilpotents. Et elle est compatible avec la réduction de Jordan. Cette approche est générale à l'analyse des endomorphismes. Dans le cas des endomorphismes nilpotents, elle est intimement liée à la notion de base réduite. Tout endomorphisme nilpotent u d'un espace vectoriel E non réduit au vecteur nul vérifie les propriétés suivantes :
-
- Si
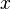
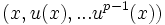
- Pour tout sous-espace stable F de E (en particulier pour tout sous-espace cyclique), l'endomorphisme de F obtenu par restriction de u est, lui aussi, nilpotent (donc vérifie toutes les propriétés de cette liste, dès que F n'est pas réduit au vecteur nul).
- u possède une unique valeur propre : 0 (en particulier, son noyau n'est pas réduit au vecteur nul).
- E est somme directe de sous-espaces cycliques non réduits au vecteur nul.
- Une telle décomposition est "maximale", au sens où toute autre décomposition de E en somme directe de sous-espaces stables non réduits au vecteur nul est constituée d'au plus autant de sous-espaces.
- Si
-
- Un endomorphisme u est nilpotent si et seulement si son polynôme minimal est égal à Xp ou p est l'indice de l'endomorphisme.
Par définition de la nilpotence, Xp est un polynôme annulateur de l'endomorphisme u, et ce n'est le cas d'aucun de ses diviseurs stricts. Comme
![\mathbb K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/11cf18672fa8c102e5d2ec8bdfe203c8_bd379140d6a603f16bfb95868779a783.png)
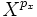
-
- Si x est un vecteur d'indice px alors la famille
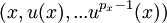
- Si x est un vecteur d'indice px alors la famille
-
- Il existe toujours un vecteur dont l'indice est celui de l'endomorphisme.
En effet le polynôme minimal d'un vecteur divise le polynôme minimal de l'endomorphisme, donc est un Xk, pour k ≤ p, et si aucun n'était de degré p, Xp − 1 annulerait u.
-
- L'indice d'un endomorphisme nilpotent est toujours inférieur ou égal à la dimension de l'espace.
Cette proposition est une conséquence directe des deux résultats précédents.
-
- E est somme directe de sous-espaces cycliques (que l'on peut alors supposer tous différents de {0}, quitte "gommer" de cette somme les sous-espaces égaux à {0}).
Démontrons ce résultat par récurrence sur l'indice p de l'endomorphisme.
Si p est égal à 1, l'endomorphisme est nul et le résultat est trivial.
Supposons le résultat vrai pour p et démontrons le pour p+1. Soit u un endomorphisme d'indice p+1. Considérons alors la restriction de u à u(E). C'est un endomorphisme nilpotent d'indice p. Par hypothèse de récurrence, u(E) est somme directe de sous-espaces cycliques Fi pour i appartenant à un certain ensemble I d'indices. Chaque Fi admet une base de la forme
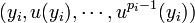
La famille
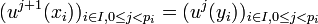
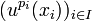
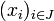

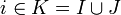
Montrons que E est la somme directe des sous-espaces cycliques associés à tous ces xi, c'est-à-dire montrons que
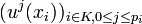
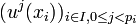
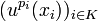
-
- La restriction de u à Ei est de noyau non réduit au vecteur nul et possède une unique valeur propre 0. Cette propriété reste vraie pour l'endomorphisme lui-même.
La restriction de u à Ei est un endomorphisme nilpotent, son polynôme minimal est une puissance de X, la seule valeur propre est 0 et comme 0 est valeur propre, le noyau est non nul. Ce raisonnement s'applique aussi à u sur l'espace vectoriel entier, ce qui démontre la fin de la proposition.
-
- Un endomorphisme est nilpotent si et seulement si son polynôme caractéristique est égal à ( − X)n ou n est la dimension de l'espace.
La seule valeur propre est 0, donc sur sa clôture algébrique, le polynôme caractéristique est scindé et possède pour racine uniquement 0. Ce polynôme est donc une puissance de X, et de degré n. Son signe provient du signe du monôme de plus haut degré de tous les polynômes caractéristiques.