Référentiel galiléen - Définition

Changement de référentiel

Un changement de référentiel est l'ensemble des lois à appliquer pour convertir les grandeurs physiques d'un référentiel à un autre. Dans le cas où la conversion porte sur les distances et les durées, on parle de transformation.

Mécanique classique

Dans le cadre de la mécanique newtonienne, si un référentiel est animé d'un mouvement relatif de translation rectiligne uniforme par rapport à un référentiel inertiel, alors ce référentiel est lui-même inertiel : les corps libres y sont aussi soumis au « mouvement inertiel ». Il existe donc une infinité de référentiels inertiels en translation rectiligne uniforme les uns par rapport aux autres, et on admet que tous les référentiels inertiels le sont.

Si les , pour i = 1;2, désignent les deux référentiels inertiels d'origines respectives , et les désignent les vecteurs joignant les origines au point du corps observé, les les temps homogènes dans chaque référentiel, et la vitesse relative de par rapport à , la formule vectorielle de changement de référentiel est :

, en prenant du fait de la première égalité.

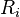
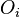
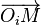
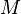
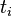
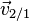
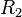
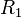
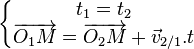
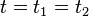
Si les axes des référentiels sont deux à deux parallèles et la vitesse relative est parallèle à l'axe des , on obtient :

Relativité restreinte

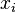
Dans cette théorie aussi, on admet comme hypothèse que tous les référentiels galiléens sont en translation spatiale rectiligne uniforme les uns par rapport aux autres. La différence avec la physique classique est que ce sont des référentiels de l'espace de Minkowski à quatre dimensions et que l'axe du temps est propre à chaque référentiel.

Les transformations de Lorentz coïncident avec les transformations de Galilée pour des vitesses faibles par rapport à la vitesse de la lumière.

Critique par Henri Poincaré

Henri Poincaré dans son livre La Science et l'Hypothèse (1902) a souligné que les principes de la physique ne sont fondés sur aucune nécessité logique.

Déjà, ce savant mettait en cause l'a priori que l'espace physique est un espace euclidien à trois dimensions, bien qu'il ait conclu « Aucune expérience ne sera jamais en contradiction avec le postulatum d'Euclide ; en revanche aucune expérience ne sera jamais en contradiction avec le postulatum de Lobatchevsky ». On sait depuis la relativité restreinte, et plus encore depuis la relativité générale, combien ses doutes étaient fondés.

Poincaré articule sa réflexion comme suit. Un référentiel galiléen est défini comme un référentiel cartésien, de l'espace supposé affine, dans lequel le mouvement de tout corps non influencé par une force est rectiligne uniforme : il faut savoir ce qu'est une force avant de poser cette définition. Une force ne peut être mesurée -donc définie- que par le fait qu'elle rend le mouvement non rectiligne-uniforme : la notion de force présuppose que celle de référentiel galiléen est bien définie. La force et le référentiel inertiel sont définis l'un par l'autre. Ce qui ressemble dès lors à une définition circulaire trouve sa justification dans les expériences : en observant des systèmes à peu près isolés (c'est-à-dire loin de tout corps pouvant l'influencer de manière significative), on arrive toujours à définir des référentiels dans lesquels les mouvements des centres de gravité des systèmes sont à peu près rectilignes et uniformes. Enfin, Henri Poincaré insiste : la mécanique est une science expérimentale où la nature des notions utilisées importe peu, seuls comptent le fait que ces notions soient « commodes » du point de vue de leur formulation mathématique, qu'elles soient mesurables et permettent de prédire des résultats d'expériences renouvelées.

L'exemple typique de la définition circulaire est le référentiel lié au sol terrestre : dans ce référentiel la chute des corps ne peut pas être négligée comme peuvent l'être les frottements de l'air, ou la tendance à la fuite centrifuge des corps due à la rotation de la terre sur elle-même, mais si on identifie cette chute des corps comme un effet dû à une force dont les propriétés doivent être déterminées, ce référentiel peut être considéré comme approximativement -et pour une expérience de courte durée- galiléen et soumis à la force de gravitation. Avec l'analyse d'Einstein du principe d'équivalence, il apparaît que comme la gravitation soumet tous les corps au même effet, on peut considérer qu'elle est due aux propriétés de l'espace et que, dès lors, un référentiel lié au sol terrestre n'est pas doté d'un environnement homogène et isotrope, donc ne peut pas être considéré comme galiléen : les seuls véritables référentiels galiléens sont ceux qui sont en chute libre (bien qu'ils ne soient que localement galiléens). Le travail d'Einstein aboutit à la relativité générale qui est plus proche des observations récentes que la loi universelle de la gravitation de Newton.