Relation d'équivalence - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La notion de relation d'équivalence sur un ensemble permet de mettre en relation des éléments qui sont similaires par une certaine propriété.
On pourra ainsi regrouper ces éléments par « paquets » d'éléments qui se ressemblent, définissant ainsi la notion de classe d'équivalence, pour enfin construire de nouveaux ensembles en « assimilant » les éléments similaires à un seul et même élément. On aboutit alors à la notion d'ensemble quotient.
Définition
Définition formelle
Une relation d'équivalence
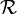
- C'est une relation binaire : c'est donc une somme disjointe
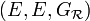
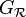
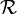
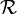
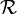
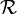
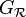
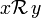
-
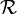
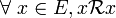
-
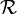
-
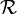
Définition équivalente
On peut aussi définir une relation d'équivalence comme une relation binaire réflexive et circulaire.
Une relation binaire est circulaire ssi toute image d'une image d'un élément de E est antécédent de cet élément, c'est-à-dire si :
Ensemble quotient
C'est l'ensemble des classes d'équivalence de E suivant

Définition
L' ensemble quotient de E par la relation d'équivalence

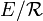

L'ensemble quotient est donc un nouvel ensemble construit à partir de E et de

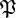
Remarque : on peut munir une classe propre d'une relation d'équivalence. On peut même y définir des classes d'équivalence, mais comme elles peuvent être elles-mêmes des classes propres, cela interdit l'existence d'un ensemble quotient dans ce cas. Par exemple, si l'on considère la relation d'équipotence dans la classe des ensembles, cette relation est une relation d'équivalence, et on peut y définir des classes d'équivalence dites « classes d'équipotence » :
- la classe d'équipotence de l'ensemble vide est ainsi le singleton formé par l'ensemble vide, puisqu'il ne peut être mis en bijection qu'avec lui-même;
- les singletons forment une autre classe d'équipotence; mais il s'agit d'une classe propre, ce qui interdit de former un ensemble ( ou une classe ) à partir des classes d'équipotence ( et, accessoirement, d'identifier les classes d'équipotence aux cardinaux ).
L'ensemble quotient peut aussi être désigné comme « l'ensemble E quotienté par


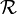
Exemple
L'ensemble des entiers relatifs peut être muni de la relation « a le même signe que » (comprise au sens strict). Il y a trois classes d'équivalence :
- l'ensemble
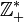
- l'ensemble
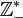
- le singleton {0}.
On peut noter ces trois classes par, respectivement, (+), (-) et (0).
On connaît la « règle des signes » pour le produit de deux entiers relatifs : elle montre que si on sait dans quelle classe d'équivalence se trouvent x et y, le produit xy se trouve dans une classe bien déterminée. Par exemple, si x est dans (+) et y dans (0), alors xy est dans (0). Formellement, on peut le noter (+)·(0)=(0). De même (+)·(-)=(-), ou encore (+)·(+)=(+), (-)·(-)=(+) etc. Ceci est un exemple simple de loi-quotient.
Mais avec cet exemple on ne peut pas « faire passer au quotient » la loi + : que dire de la somme d'un élément de (+) et d'un élément de (-) ? Pour savoir si les lois et les propriétés de structure sont compatibles avec le passage au quotient, il est utile d'introduire le concept de surjection canonique.
Surjection canonique
Il existe une surjection canonique s de E dans l'ensemble quotient, qui à chaque élément de E associe sa classe d'équivalence :
- s :
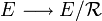
-
s est une application puisque tout élément de E appartient à une et une seule classe d'équivalence; s est surjective puisqu'aucune classe d'équivalence n'est vide.
s n'est pas en général injective, mais on a :
Cette surjection est ainsi une bijection ssi la relation d'équivalence concernée n'est autre que la relation d'égalité.
Structure quotient
Grâce à la surjection s , si E est muni d'une structure, il est possible de transférer cette dernière à l'ensemble quotient, sous réserve que la structure soit compatible avec la relation d'équivalence, c'est-à-dire que deux éléments de E se comportent de la même manière vis-à-vis de la structure s'ils appartiennent à la même classe d'équivalence. L'ensemble quotient est alors muni de la structure quotient de la structure initiale par la relation d'équivalence.
Par exemple, si E est muni d'une structure de groupe, il est possible, dans certains cas, de parler du groupe quotient
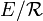
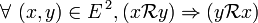
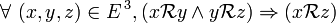
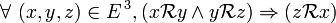
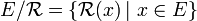
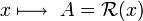
![\forall x \in E , \forall y \in E , \, [ s ( x ) = s ( y ) ] \Leftrightarrow [ \mathcal R ( x ) = \mathcal R ( y ) ] \Leftrightarrow [ x \mathcal R y ] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c78c02d3c566a6d5aeb7c4db2a87e43a_940e00ddd9dcd7f762f5efee984d56e5.png)

















































