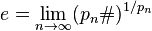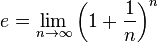Représentations de e - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| la constante mathématique e | |
|---|---|
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
Cet article porte sur les représentations de e, une importante constante mathématique.
Elle peut être définie de différentes manières en tant que nombre réel. Puisque e est un nombre irrationnel, elle ne peut être représentée par une fraction ordinaire, mais bien par une fraction continue. En s'appuyant sur les résultats du calcul infinitésimal, e peut aussi être calculée à partir d'une série infinie, d'un produit infini et de plusieurs limites de suite.
Comme fraction continue
La constante e peut être représentée comme fraction continue simple (une démonstration est proposée dans l'article Fraction continue. Voir aussi suite A003417 de l’OEIS) :
Voici quelques fractions continues généralisées de e. La deuxième est obtenue en effectuant une transformation d'équivalence. La troisième – contenant… 6, 10, 14, … – converge très rapidement.
Posant m=x et n=2 donne
Comme produit infini
La constante e est aussi donnée par plusieurs produits infinis, dont le produit de Pippenger :
et le produit de Guillera
où le ne facteur est la ne racine du produit
Il y a aussi les produits infinis
et
Comme séries infinies
La constante e est aussi égale à la somme de ces séries infinies :
-
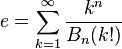
(Pour les séries infinies 2 à 7, voir)
Comme limite d'une suite
La constante e est égale à plusieurs limites de suite infinies :
-
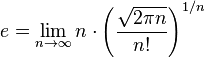
(Les deux sont obtenues par la formule de Stirling).
La limite symétrique,
peut être obtenue en manipulant la limite de base de e. Une autre limite :
où pn est le ne nombre premier et
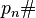
Probablement la limite la plus connue :
![e = [2; 1, \textbf{2}, 1, 1, \textbf{4}, 1, 1, \textbf{6}, 1, 1, \textbf{8}, 1, \ldots,1, \textbf{2n}, 1,\ldots] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c5cd8a88b6f65d68bb2cde6c3b19a450_e93b0ef1829bf1cee4d13217e385eb87.png)
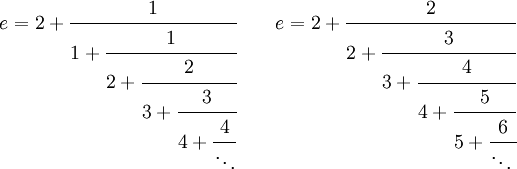
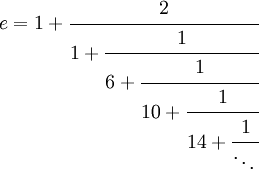
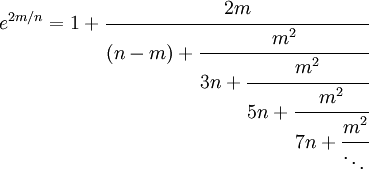
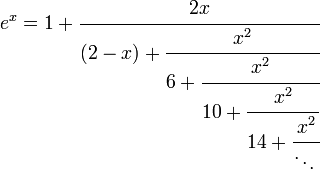
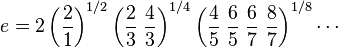
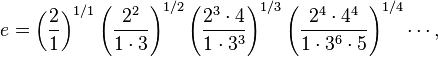
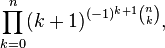
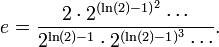
![e=\sqrt[1]{\frac{2}{1}}\cdot\sqrt[2]{\frac{4}{3}}\cdot\sqrt[4]{\frac{6\cdot 8}{5\cdot 7}}\cdot\sqrt[8]{\frac{10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\cdots](https://static.techno-science.net/illustration/Definitions/autres/c/cf562e91091a5e52d0e3d117a573e394_71f54dea060cdcaf3b6e4ee9d8daf191.png)
![e = \left [ \sum_{k=0}^\infty \frac{(-1)^k}{k!} \right ]^{-1}](https://static.techno-science.net/illustration/Definitions/autres/a/aee6e89e7dadfca2d0f4ab8ef07da7e2_cff138adab62f7777b085621bd83d159.png)
![e = \left [ \sum_{k=0}^\infty \frac{1-2k}{(2k)!} \right ]^{-1}](https://static.techno-science.net/illustration/Definitions/autres/3/347be98b47bdc3e043fe243d36c189c9_9ca622c7b2936395fdb3ce0cb8f6759a.png)
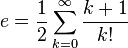
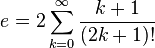
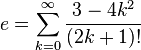
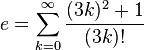
![e = \left [ \sum_{k=0}^\infty \frac{4k+3}{2^{2k+1}\,(2k+1)!} \right ]^2](https://static.techno-science.net/illustration/Definitions/autres/6/6c4187bccdf5b7cea4115c87ffa31868_436dd7c68ddfc7485f0fbfd19a1e9fce.png)
![e = -\frac{12}{\pi^2} \left [ \sum_{k=1}^\infty \frac{1}{k^2} \ \cos \left ( \frac{9}{k\pi+\sqrt{k^2\pi^2-9}} \right ) \right ]^{-1/3}](https://static.techno-science.net/illustration/Definitions/autres/9/9c16e1799809ea1ab294b06efd76be16_9687436b6abadf8e95bd4c01e9ec2e19.png)
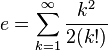
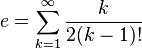
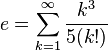
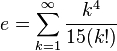
![e=\lim_{n \to \infty} \frac{n}{\sqrt[n]{n!}}](https://static.techno-science.net/illustration/Definitions/autres/1/1ece0ee65e250a7a3ec0a38140ef258c_e97bbfa8ac2ffe4d3049d4122e415ada.png)
![e=\lim_{n \to \infty} \left [ \frac{(n+1)^{n+1}}{n^n}- \frac{n^n}{(n-1)^{n-1}} \right ]](https://static.techno-science.net/illustration/Definitions/autres/a/a5a7a2f503a54c1cfaf249f1fa146ebc_b31b5acf29f0c5f02e1c99e508dc1c4e.png)