Semi-anneau d'ensembles - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un semi-anneau d'ensembles (généralement abrégé en semi-anneau) est une classe de parties d'un ensemble X à partir de laquelle on construit facilement un anneau d'ensembles. C'est un cadre commode pour commencer plusieurs constructions classiques de mesures.
Définition
Définition — Un semi-anneau d'ensembles est un ensemble
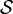
- L'ensemble vide est élément de
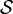
- Pour tous A, B éléments de
-
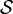
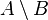
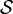
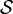
Lorsque de surcroît l'ensemble X est élément de
Extension d'une mesure d'un semi-anneau à un anneau
L'anneau d'ensembles engendré par un semi-anneau se décrit facilement :
Proposition — Le plus petit anneau d'ensembles qui contienne un semi-anneau
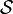
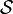
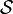
Dans l'énoncé d'extension qui suit, on entend par « mesure » sur une classe
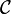
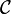
![[0,+\infty]](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0dc741c63f937db1bb20cfbcb633b71c_f7f63f9efef126b9fedf2310058eec21.png)
Proposition — Soit
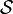
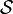
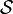
L'unicité est claire, vu l'additivité des mesures et la description des éléments de l'anneau engendré par
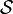
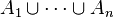
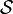
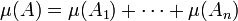
Les énoncés analogues utilisant des semi-algèbres au lieu des semi-anneaux et des algèbres d'ensembles au lieu des anneaux d'ensembles sont également vrais, et se déduisent aussitôt de ceux qui sont donnés ici. L'usage des uns ou des autres est souvent indifférent : travailler sur des semi-algèbres est cohérent avec l'objectif terminal de construire une mesure sur une σ-algèbre et évite d'avoir à introduire le concept supplémentaire d'« anneau » ; travailler sur des semi-anneaux permet d'alléger la vérification initiale de σ-additivité et se justifie par ailleurs pleinement quand on a pour objectif de construire des mesures sur des σ-anneaux ou δ-anneaux.
Exemples
- L'ensemble des intervalles de
- L'ensemble des intervalles bornés de
- L'ensemble des intervalles vides ou de la forme ]a,b] (a < b) est un semi-anneau inclus dans le précédent.
- Étant donnés deux semi-anneaux
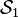
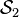
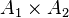
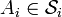
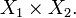
![]a_1,b_1]\times\cdots\times]a_n,b_n]](https://static.techno-science.net/illustration/Definitions/autres/f/f7b912c86adddfce2b35613a3ffcd42d_ca7f197d6d63b2821269d19393c51c66.png)
![]a_1,b_1]\times\cdots\times]a_n,b_n]](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f7b912c86adddfce2b35613a3ffcd42d_ca7f197d6d63b2821269d19393c51c66.png)
Exemples d'utilisation de semi-anneaux
Construction de la mesure de Lebesgue sur l'espace à n dimensions
Un des modes de construction de la mesure de Lebesgue sur
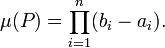
On étend ensuite cette définition à la classe des ensembles Lebesgue-mesurables.
Cette construction débute par l'invocation, explicite ou implicite, de la proposition énoncée ci-dessus afin d'étendre dans un premier temps la mesure à l'anneau d'ensembles de toutes les unions d'intervalles bornés. L'intérêt des semi-anneaux apparaît nettement ici, car les énoncés qui précèdent, complétés par le théorème d'extension de Carathéodory pour l'étape suivante de l'extension, montrent que la σ-additivité de la mesure découle in fine d'une vérification de σ-additivité où on peut se limiter à manipuler des pavés.
On trouvera ci-dessous en boîte déroulante le détail de cette vérification, qui n'est pas triviale et fournit un exemple de manipulations sur un semi-anneau.
Notons
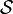
On montre d'abord que μ est additive, au sens suivant : si P est un pavé dans
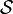
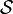
On doit ensuite montrer que μ est une mesure, c'est-à-dire qu'elle est σ-additive. Pour le prouver, soit donc un pavé P élément de
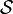
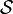
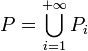
On doit montrer l'égalité :
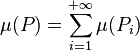
L'inégalité dans un sens ne demande pas d'idée particulièrement ingénieuse. Pour r fixé, la différence
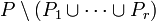
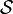
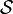
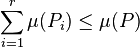
En faisant tendre r vers l'infini on conclut :
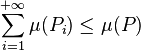
L'inégalité réciproque repose sur des considérations topologiques touchant à la régularité de la mesure de Lebesgue. On commence par fixer un ε > 0 et inclure chaque Pi dans un pavé Qi produit d'intervalles ouverts dont le volume soit inférieur ou égal à μ(Pi) + ε / 2i. De la même façon, on considère un pavé Q produit d'intervalles fermés, contenu dans P et dont le volume soit supérieur ou égal à μ(P) − ε.
Le pavé Q est compact comme fermé borné de
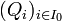
Par additivité finie et positivité de μ sur le semi-anneau
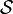
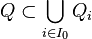
fournit l'inégalité :
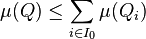
et a fortiori :
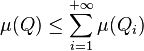
qu'on peut incorporer dans la chaîne d'inégalités :
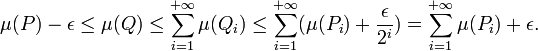
Il n'y a plus qu'à faire tendre ε vers 0 pour conclure.
Construction de mesures sur la droite réelle par le procédé de Stieltjes
Toute mesure localement finie sur la droite réelle peut se construire par un procédé généralisant celui exposé ci-avant. Il est opportun d'utiliser le semi-anneau des intervalles vides ou de la forme ]a,b] (a < b).
Pour toute fonction croissante de
mesure qu'il est ensuite possible d'étendre à la tribu borélienne de
La méthode se généralise à toute dimension finie.
