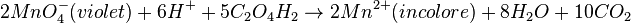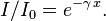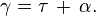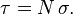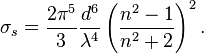Spectrophotométrie - Définition

Applications

Détermination d'une concentration inconnue

Connaissant le spectre d'absorption d'une espèce chimique, on peut mesurer, à l'une de ses longueurs d'onde (là où l'absorption est maximale) les variations de l'intensité d'un faisceau lumineux traversant une même épaisseur de solutions de concentrations diverses.

Courbe d'étalonnage

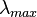
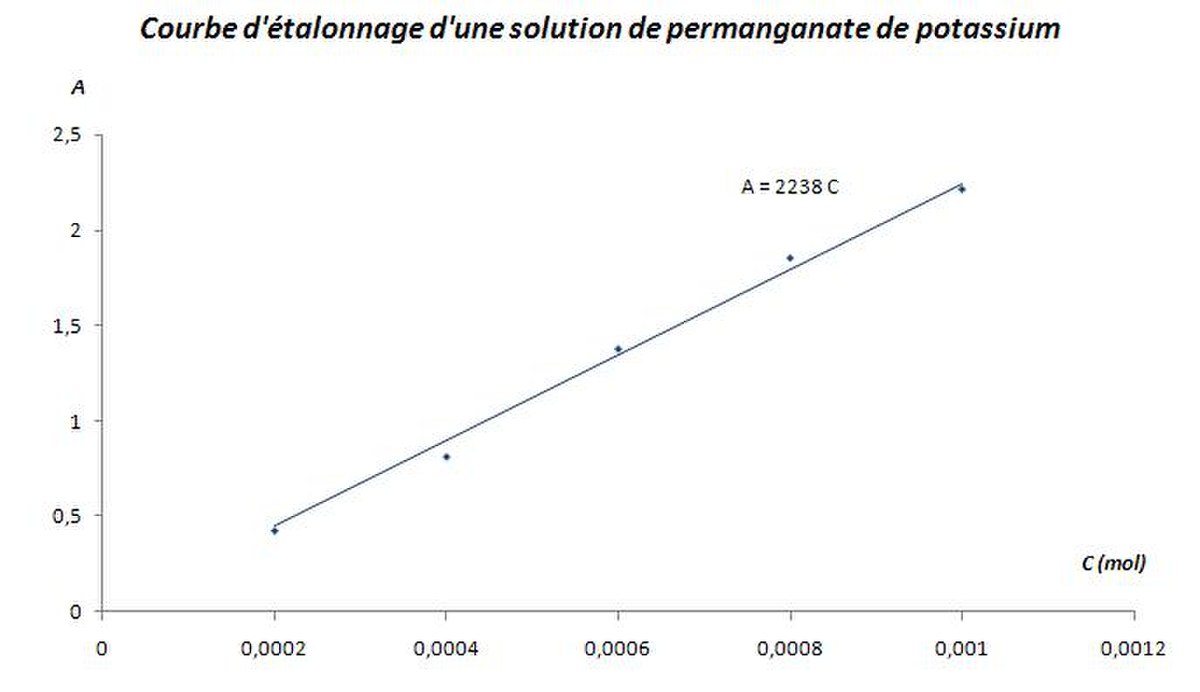
Ceci permet d'établir expérimentalement la courbe reliant l'absorbance et la concentration de la substance étudiée (avec ), en effectuant les mesures de pour diverses concentrations. Cette courbe est une courbe d'étalonnage.

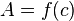
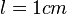
La courbe expérimentale d'étalonnage permet ensuite de déterminer la concentration inconnue d'une solution de cette substance par simple mesure de son absorbance et report sur le graphe .

La loi de Lambert-Beer a des limites. Elle n'est linéaire que dans un intervalle de concentrations réduit regroupant des valeurs inférieures à 10^-2mol.l^-1.

Suivi cinétique

Suivi de la cinétique d'une réaction chimique

Lorsqu'au cours d'une réaction chimique dont on veut étudier la cinétique de l'une des espèces chimique en solution, on peut par spectrophotométrie d'absorption suivre la concentration de cette espèce (généralement colorée). Si cette espèce est un réactif, l'absorbance de la solution diminue au cours du temps. Si au contraire, c'est un produit de la réaction, l'absorbance de la solution augmente au cours du temps.

Exemples

• On peut suivre la cinétique de la réaction d'oxydo-réduction en milieu acide, entre l'acide oxalique C₂H₂O₄ par l'ion permanganate MnO₄^- (couleur violette) par la mesure de la diminution d'absorbance de ce dernier pour la longueur d'onde λ = 540 nm.

Limites

Plusieurs facteurs peuvent dégrader la loi de Beer-Lambert et limiter la validité de la spectrophotométrie :

• Le domaine de mesure idéal est pour les valeurs de T situées entre 20 et 60%.
• Plusieurs aberrations optiques liés à la diffusion, la réflexion et la diffraction de la lumière peuvent fausser la mesure.
• Les phénomènes de fluorescence ainsi que d'autres particularités chimiques liées aux espèces absorbantes peuvent interférer.
• Plus la densité du soluté est importante, plus le faisceau de lumière incident sera réfracté avec une valeur donnée. Cette tendance est normalement infime mais devient plus prononcée avec les hautes concentrations. Ainsi, la réfraction réduit l'intensité de la lumière transmise et l'instrument indique faussement une absorbance plus élevée. Généralement, ce phénomène peut être évité en travaillant avec des concentrations inférieures à 0,01 mol.l^-1.

Importance du phénomène de diffusion

Comme la loi de Beer-Lambert le stipule, le pouvoir d'un milieu à bloquer le passage de la lumière est quantifié par un coefficient d'extinction donné par l'équation :

Cette impédance est générée par deux phénomènes distincts : l'absorbance et la diffusion.

• La diffusion intervient lorsque la lumière est défléchie par les particules du milieu de manière à ne pas atteindre l'autre côté de l'échantillon.
• L'absorbance est le processus par lequel l'énergie lumineuse est absorbée par les molécules de l'échantillon avant d'être libérée sous forme de chaleur ou emmagasinée sous forme de liaisons chimiques.

Donc que le coefficient de l'équation précédente est composé par le coefficient de diffusion ( ) ainsi que celui de l'absorption ( ), c'est-à-dire :

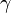
Le coefficient de diffusion peut être exprimé par le produit de la concentration des particules, , et la section efficace de celles-ci, (à supposer que ces particules sont homogènes et régulièrement réparties dans le milieu), on a :

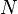
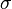
La section efficace, qui est une mesure de la proportion de lumière diffusé par particule, est fonction de leur taille. En effet, pour les particules de petite taille (p. ex. leur diamètre représente 10% de la longueur d'onde incidente) la diffusion de Rayleigh prédomine. La diffusion de Rayleigh dépend de la longueur du parcours, de la concentration des particules diffusantes, de la longueur d'onde et de la polarisation de cette dernière. Pour une particule idéalement sphérique, la section efficace de Rayleigh s'écrit :

• est le diamètre des particules,
• est la longueur d'onde,
• est l'indice de réfraction.

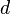
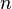
Cette équation prédit que les courtes longueur d'ondes seront les plus diffusées.
Pour des particules plus grosses que la longueur d'onde, elles font l'objet d'un phénomène plus complexe appelé diffusion de Mie. Puisque la lumière sera diffusée selon différents angles, dans ce cas la forme des particules doit être prise en compte dans la section efficace. La section efficace maximale est obtenu quand la taille de la particule est proche de la longueur d'onde incidente. La diffusion diminue de plus en plus que la différence entre la taille de la particule et la longueur d'onde augmente (c'est le cas de la spectrophotométrie moléculaire).