Statistique descriptive - Définition

Exemples

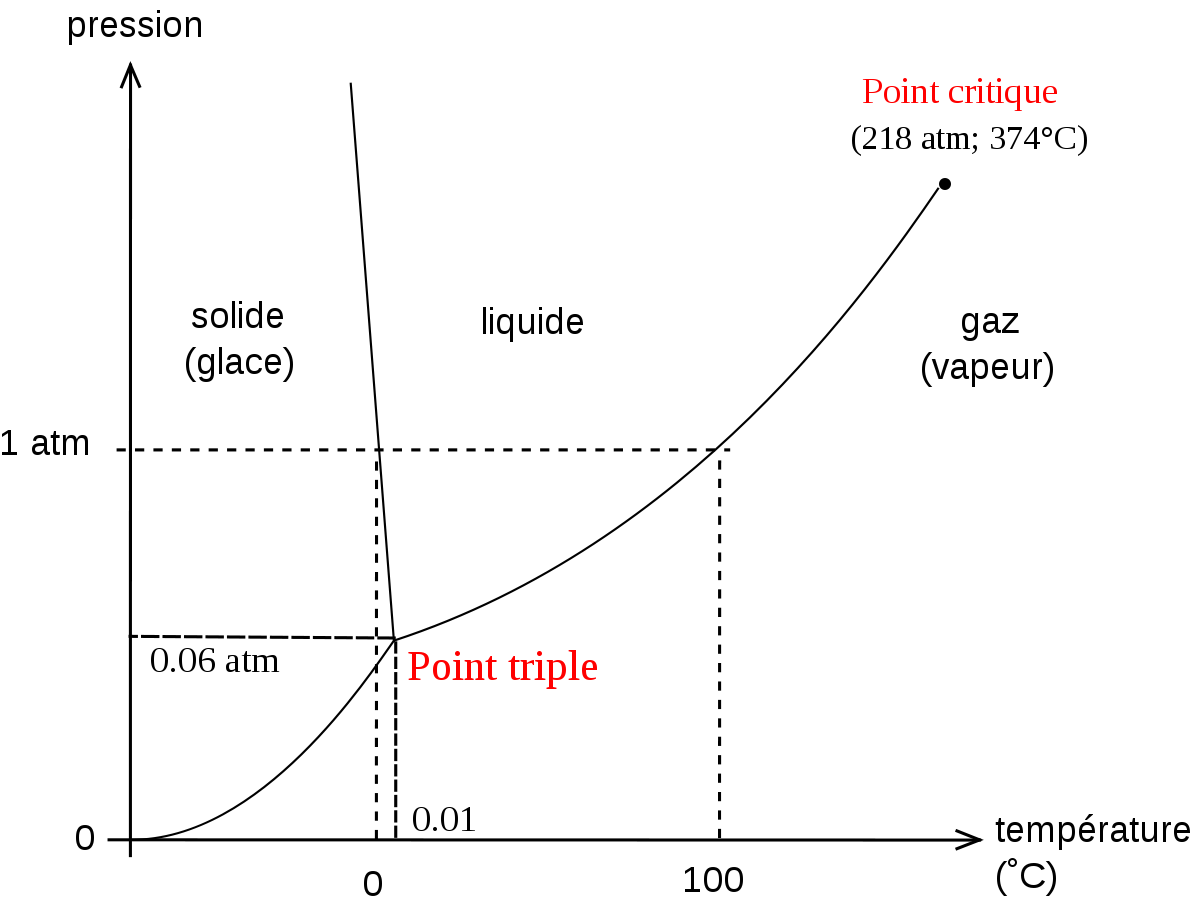
Grandeurs physiques

Diagramme de phase de l'eau.

Si on mesure de temps à autre la pression, la température et la densité d'un gaz présent dans une cuve, on obtient une collection de triplets de données, indexés par l'instant de mesure.

Grandeurs comportementales ou biologiques

Dans le domaine médical, on peut par exemple mesurer le poids avant et après la prise d'un médicament pour plusieurs personnes. On obtient alors une collection de couples de données (poids avant et après) indexés par le nom de la personne.

En sociologie ou en marketing on peut mesurer le nombre de livres lus par an pour de nombreuses personnes, dont on connait par ailleurs l'âge et le niveau d'étude. Ici aussi on obtient une collection de triplets de données, indexés par le nom du lecteur.

Formalisation des cas pratiques

Les différentes grandeurs mesurées sont appelées des variables.

L'étude statistique nécessite que l'on prenne comme hypothèse qu'il existe un phénomène abstrait plus ou moins caché qui met en œuvre ces variables (et peut-être d'autres).

Chaque valeur l'index (qui peut être une date, ou un numéro identifiant un individu), identifie alors une photographie partielle du phénomène. On appelle les valeurs des variables pour un indice donné des observations ou une réalisation du phénomène.

D'un point de vue formel, on pose le principe que le phénomène abstrait peut comporter des éléments déterministes comme des éléments aléatoires (on dit aussi stochastiques). L'ensemble des variables observées sont alors juxtaposées sous la forme d'un vecteur de données. Il n'y a plus alors qu'une seule variable (mais qui est multi variée).

Les observations sont alors bien des réalisations (au sens des statistiques mathématiques) de cette variable aléatoire multi variée.

Étude de plusieurs variables

Le principe est le même que pour une seule variable, sauf que toutes les caractéristiques (moyenne, mode, écart type, etc) sont bi variées (des vecteurs).

Il y a d'autre part une caractéristique supplémentaire: la corrélation. Elle est une mesure linéaire de la dépendance entre les différentes composantes de la variable multi variée.

Il existe d'autres mesures de dépendance entre deux variables, comme l'information mutuelle (ou l'entropie conditionnelle).

Au delà des mesures, on peut aussi explorer les dépendances à l'aides d'outils graphiques ou de tableaux.

Disjonction des données

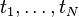
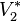
Le plus simple des tableaux possible est une disjonction. Lorsque nous avons deux variables V₁ et V₂, observées par exemple en plusieurs instants (notons (V₁(t_n),V₂(t_n)) l'observation des deux variables à l'instant t_n), il est toujours possible de choisir un seuil sur la deuxième variable et de transformer notre échantillon (V₁(t_n),V₂(t_n))_n en . Nous formons alors deux groupes d'instants :

1. ceux pour lesquels la seconde variable est plus grande que ;
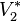
2. ceux pour lesquels la seconde variable est plus petite ou égale à .

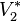
Plus ces deux ensembles seront différents (en termes de critère mono variés: moyenne, écart type, comparaison à une distribution connue, etc), et plus l'événement a un impact sur la distribution des valeurs de V₁. Lorsque c'est le cas, nous avons identifié une dépendance entre V₁ et l'événement .

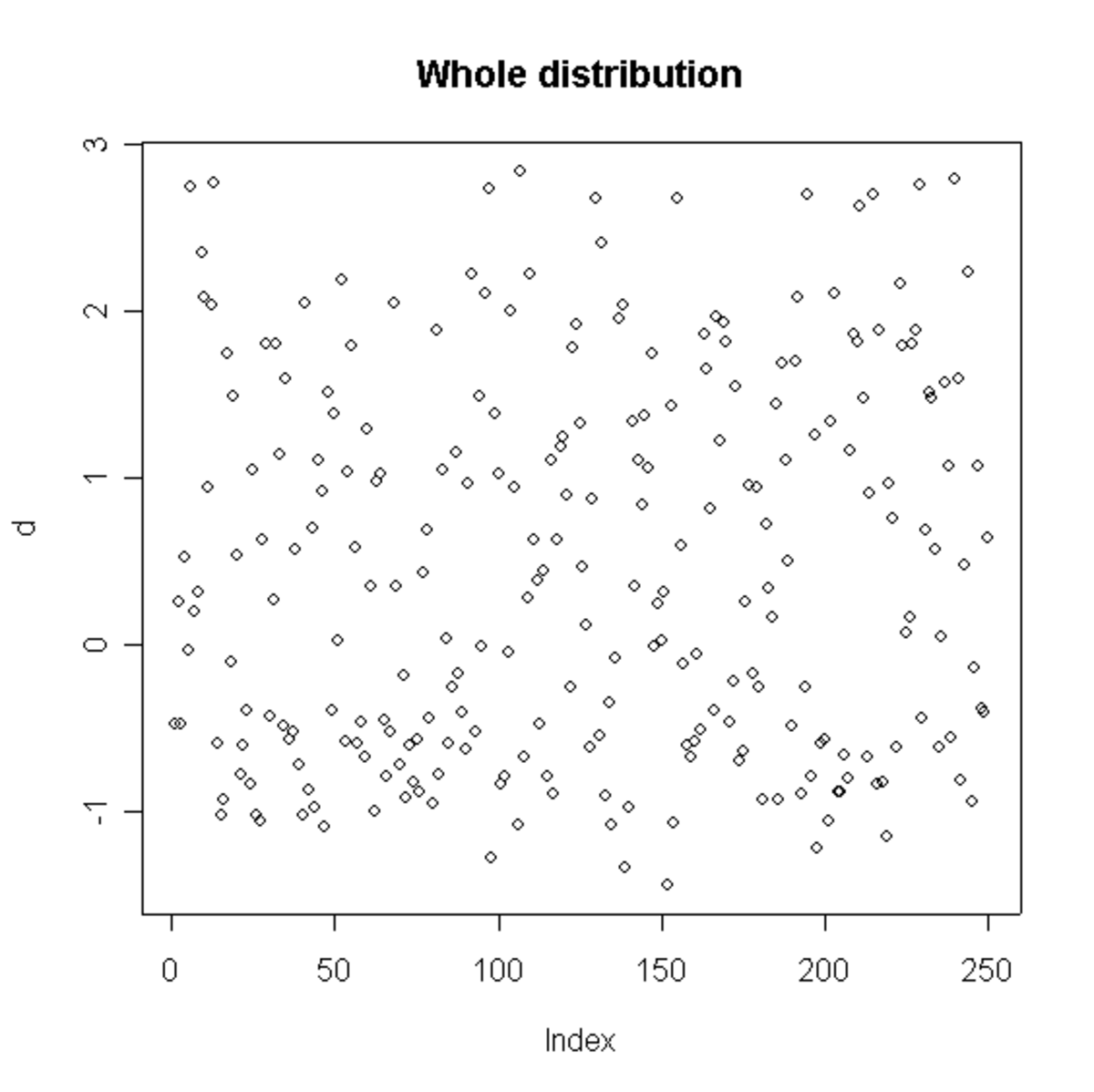
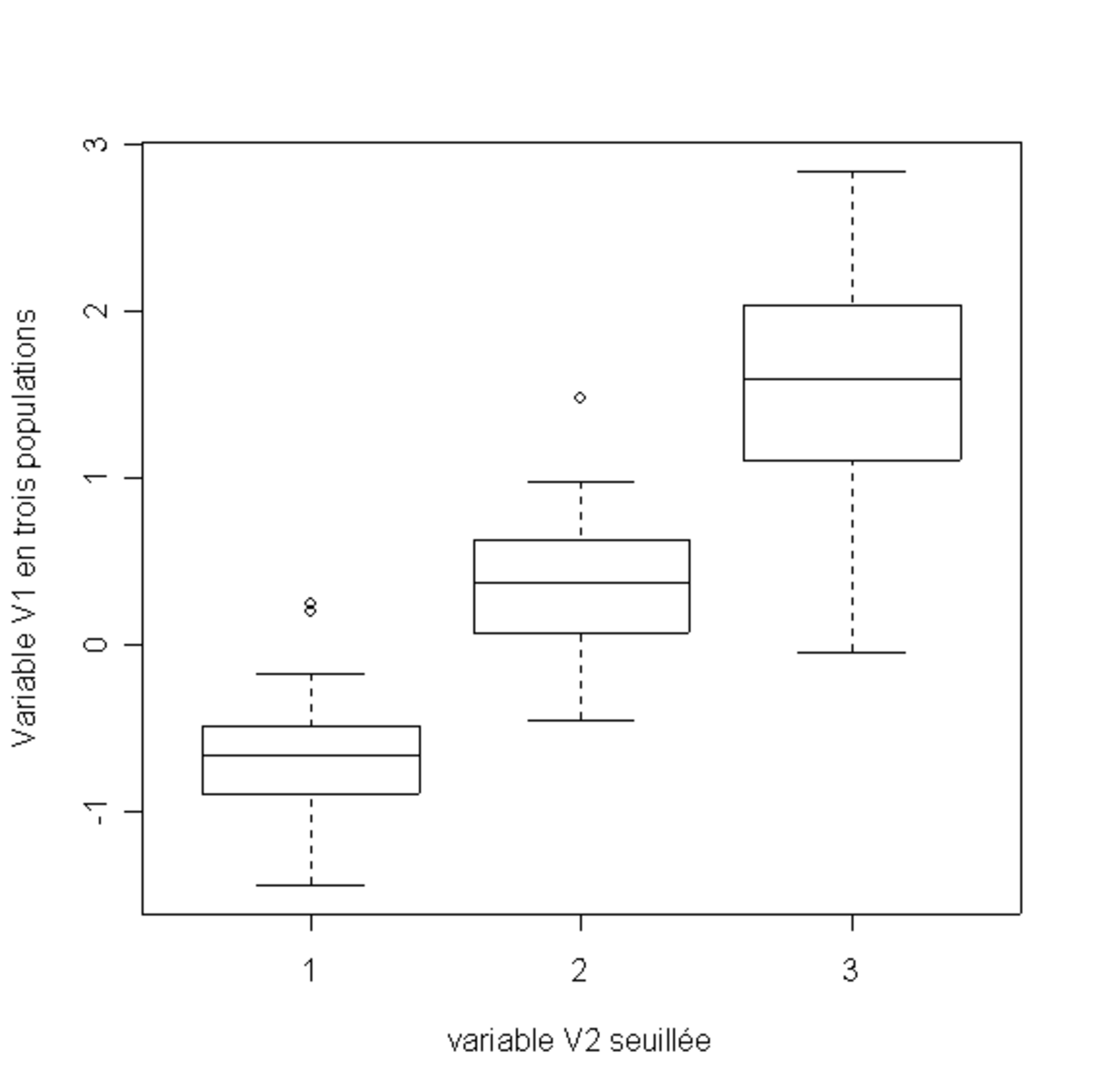
Il est possible de poursuivre cela en découpant notre échantillon en plusieurs morceaux, en recourant à plusieurs seuils .

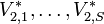
On se retrouve alors avec une population de S + 1 échantillons à une seule variable (V₁), qui peuvent être étudiés séparément. Si on s'aperçoit que les distributions sur les échantillons sont très différentes, c'est qu'il y a une dépendance entre les deux variables.

Une population aléatoire (la deuxième variable n'est pas affichée)

Après seuillage de la deuxième variable: trois groupes sont formés. On voit nettement que les trois distributions sont très différentes; il y a donc bien une dépendance entre les deux variables