Statistique descriptive - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La statistique descriptive est la branche des statistiques qui regroupe les nombreuses techniques utilisées pour décrire un ensemble relativement important de données.
Description statistique
L'objectif de la statistique descriptive est de décrire, c'est-à-dire de résumer ou représenter, par des statistiques, les données disponibles quand elles sont nombreuses.
Les données disponibles
Toute description d'un phénomène nécessite d'observer ou de connaître certaines choses sur ce phénomène.
- Les observations disponibles sont toujours constituées d'ensemble d'observations synchrones. Par exemple : une température, une pression et une mesure de densité à un instant donné dans une cuve précise. Ces trois variables synchrones peuvent être observées plusieurs fois (à plusieurs dates) en plusieurs lieux (dans plusieurs cuves).
- Les connaissances disponibles sont quant à elles constituées de formules qui relient certaines variables. Par exemple, la loi des gaz parfaits PV = nRT.
La description
Il est assez compliqué de définir la meilleure description possible d'un phénomène. Dans le cadre des statistiques, il s'agira de fournir toute l'information disponible sur le phénomène en moins de chiffres et de mots possibles.
Typiquement, la loi des gaz parfaits est une très bonne description du phénomène constitué du comportement d'un gaz en état d'équilibre dont on n'observe que la pression, la température et le volume. La valeur de la constante R peut alors être vue comme une statistique associée à cette description.
La question de la description visuelle se pose aussi, mais nous la mettrons provisoirement de côté. L'article Visualisation des données y répond plus directement.
Point de vue statistique
Le point de vue statistique sur la description d'un phénomène provient de ce que l'on considère que les observations disponibles sont différentes manifestations du même phénomène abstrait. Pour rester sur l'exemple de la température, la pression et la densité mesurées en plusieurs instants, on va considérer qu'à chaque fois que l'on prend ces trois mesures, on observe le même phénomène. Les mesures ne seront pas exactement les mêmes ; c'est la répartition de ces mesures que nous allons décrire statistiquement.
Étude d'une seule variable
Description d'un phénomène mono varié
Commençons par la situation la plus simple: celle de l'observation d'une seule variable (par exemple la pression dans une cuve, ou bien le nombre de livres lus par an pour une personne). Comme nous l'avons vu plus haut, nous prenons comme hypothèse qu'il existe un phénomène dont cette variable fait partie, que ce phénomène est peut être en partie aléatoire. Cette partie aléatoire implique que la variable observée est issue d'une variable abstraite soumise en partie à un aléa inconnu.
Les observations dont nous disposons sont alors des réalisations de cette variable aléatoire abstraite.
L'objectif des statistiques descriptives dans ce cadre est de résumer au mieux cette collection de valeurs en prenant éventuellement appui sur notre hypothèse (l'existence d'une loi aléatoire abstraite derrière tout cela).
Description exhaustive
Une première remarque est que la meilleure description possible d'un phénomène à partir d'une collection d'observations est la collection elle-même! En effet, pourquoi se compliquer la vie à calculer de nombreux indicateurs alors que tout est là?
En premier lieu, cette remarque est loin d'être stupide, et d'un certain point de vue, on retrouve cette philosophie derrière les Statistiques non paramétriques.
Mais en second lieu, on voit bien qu'il est intéressant de résumer ces observations. La question importante devient alors: comment les résumer sans détruire l'information qu'elle contient?
Exemple simple
Si nos observations sont le succès ou l'échec de 23 sportifs à une épreuve de saut en hauteur. Il s'agira d'une série de "succès" (S), "échec" (E) indexé par le nom du sportif. Voici les données:
S, S, E, E, E, S, E, S, S, S, E, E, S, E, S, E, S, S, S, S, E, E, S
Sans réfléchir et en utilisant des critères statistiques, nous pouvons décider de décrire ce phénomène comme suit:
- En attribuant un point à chacun des 23 sportifs lorsqu'il réussit son saut, et aucun lorsqu'il le rate, le nombre moyen de point gagné est 0,5652 et l'écart type des points gagné est 0,5069.
Il s'agit d'une description plutôt obscure, et on notera qu'elle comprend un peu moins de 200 caractères, alors que la liste des succès et échecs en compte moins de 50. Nous préfèrerons sans doute celle-ci:
- 23 sportifs ont sauté, 13 d'entre eux ont réussi.
Cette description est simple, claire et courte (moins de 50 caractères).
Il est aussi tout à fait possible d'en faire une description qui détruit de l'information, par exemple celle-ci:
- En attribuant un point à chaque sportif lorsqu'il réussit son saut, et aucun lorsqu'il le rate, le nombre moyen de point gagné est 0,5652
En effet, il manque au moins le nombre de sauteurs, qui est un élément descriptif important.
Bien entendu, si on cherche à décrire un phénomène particulier, comme celui-ci si j'avais parié sur un des 23 sauteurs, quelles chances avais-je de gagner?, la réponse aurait été différente:
- 57%
beaucoup plus courte, et ne détruisant aucune information au vu de la question. Il ne s'agissait plus alors de décrire les réalisations du phénomène sans point de vue particulier, mais avec un angle bien précis. On décrit en réalité un autre phénomène (celui des paris).
Il est donc très important de bien répondre à la question posée, et de ne pas appliquer des formules toutes faites sans réfléchir.
Intéressons-nous en dernier lieu à une autre question: Si je devais parier lors d'une prochaine épreuve de saut, quelles seraient mes chance de gain?.
Nous pourrions répondre 57%, comme pour la question précédente, mais après tout, nous n'avons observé que 23 sauteurs; est-ce suffisant pour en tirer une conclusion sur les performances d'autres sauteurs?
Afin d'apporter tout de même une réponse, précisons la principale hypothèse que nous allons utiliser:
- Hypothèse: la nature des performances des sauteurs sera la même que celle observée.
Cela veut dire que si cette compétition était nationale, la seconde le sera aussi: on ne va pas utiliser des observations issues d'un phénomène de niveau national avec la même phénomène, mais de niveau olympique par exemple.
Et même dans ce cadre, si par exemple nous n'avions observé que 2 sauteurs, qui avaient tout deux réussi, cela voudrait-il dire que tous les sauteurs de niveau national réussissent toujours (c'est-à-dire que j'ai une chance de gain de 100%)? Bien sûr que non.
Nous devons alors recourir à la notion d' intervalle de confiance: le but est de rendre compte de la taille de notre échantillon de sportifs, conjugué à certaines hypothèses probabilistes.
En l'occurrence, les statistiques mathématiques nous disent qu' un estimateur de proportion calculé à partir de N observations suit une loi normale de variance p(1 − p) / N autour de la proportion théorique p. Dans notre cas: N = 23 et p = 0,57. Ceci nous apprend que sous notre hypothèse, il y a une probabilité de 95% que notre chance de gain soit entre
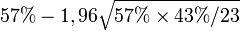
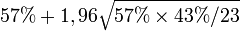
- Il y a 95% de chances que la probabilité de gagner notre pari lors d'une rencontre similaire soit comprise entre 36 et 77%
Éléments méthodologiques
Il existe finalement toute une collection de statistiques que l'on peut utiliser à des fins descriptives. Il s'agit de critères qui quantifient différentes caractéristiques de la distribution des observations:
- sont-elles centrées autour d'une valeur ?
- sont-elles groupées autour de certaines valeurs ?
- parcourent-elles de larges plages de valeurs possibles ?
- suivent-elles des lois statistiques connues?
- etc.
Sans a priori sur la question qui nous est posée, nous pouvons passer en revue ces différents indicateurs descriptifs.
Description intrinsèque d'une distribution d'observations
Sans aucun a priori sur la question que l'on se pose, quelques statistiques simples permettent de la décrire :
- la moyenne ;
- la médiane ;
- le mode ;
- le maximum ;
- le minimum ;
- l'écart type (et la variance) ;
- les quartiles.
Les deux premiers sont souvent nommés critères de position, et les autres entrent plutôt dans la catégorie des critères de dispersion.
La moyenne
La moyenne arithmétique est la somme des valeurs de la variable divisée par le nombre d'individus :
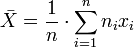
La médiane
La médiane est la valeur centrale qui partage l'échantillon en 2 groupes de même effectif : 50% au-dessus et 50% en dessous. La médiane peut avoir une valeur différente de la moyenne. En France, le salaire médian est inférieur au salaire moyen : il y a beaucoup de smicards et peu de gros salaires. Cependant, les gros salaires tirent la moyenne vers le haut.
En général, une médiane est, dans une série ordonnée, une valeur M telle qu'il y ait autant de valeurs supérieures ou égales à M que de valeur inférieures ou égales à M. exemple : 1 3 5 7 9 la médiane est 5
5 5 6 6 8 8 la médiane est égale à (6+6)/2=6
Le mode
Le mode correspond à la réalisation la plus fréquente.
Le mode d'une série, ou dominante d'une distribution, est la valeur de la variable (ou de l’unité statistique) qui revient le plus fréquemment dans la série. C'est la valeur centrale de la classe qui a le plus grand effectif.
Ex : Soit la série {8,4,4,3,4,3,8,2,5} La valeur la plus fréquente de cette série est 4. Le mode est donc égal à 4. L'effectif associé à ce mode est 3.
Il est l'indice le plus simple à déterminer puisqu'il suffit de lire un graphique ou de regarder le tableau des effectifs.
La Variance
La variance empirique corrigée
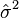
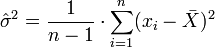
Attention : la variance (notion de statistique descriptive) égale est la simple moyenne arithmétique des carrés des écarts à la moyenne arithmétique observée, mais la variance sans biais (notion de statistique mathématique, qui signifie que en moyenne la valeur empirique est égale à la valeur théorique) est n / (n − 1) fois la variance observée. La variance sans biais est donc supérieure à la variance observée.
Écart-type
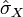
- Coefficient de variation :
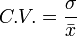
Minimum et maximum
- Étendue : c'est l'intervalle entre la plus petite et la plus grande valeur. On dit d'un phénomène qu'il présente une « forte dynamique » lorsque l'étendue (ou la dispersion) est grande.
Intervalles de confiance
La Loi des grands nombres garantit que la moyenne estimée
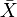
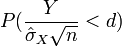
![P\left( E(X)\in \left[\bar X-\alpha {\sigma_X\over\sqrt{n}}, \bar X+\alpha {\sigma_X\over\sqrt{n}} \right]\right) = q_\alpha](https://static.techno-science.net/illustration/Definitions/autres/c/c3e3a4eb85ac81408a83424277e84790_91a8bdd96086a2cc273227b5208972a3.png)
Par conséquent, lorsque la taille de l'échantillon n augmente linéairement, la précision de l'estimateur de la moyenne augmente en
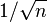
Quand l'ensemble de n points ne constitue pas un échantillon de la population, mais la population totale, la variance sans biais n'a pas à être utilisée, puisque l'on n'est plus dans un contexte d'estimation mais de mesure.
Quartiles
Ceux-ci généralisent la notion de médiane qui coupe la distribution en deux parties égales. On définit notamment les quartiles, déciles et centiles (ou percentiles) sur la population, ordonnée dans l'ordre croissant, que l'on divise en 4, 10 ou 100 parties de même effectif.
On parlera ainsi du « centile 90 » pour indiquer la valeur séparant les premiers 90% de la population des 10% restant. Ainsi, dans une population de jeunes enfants, un enfant dont la taille ou le poids est au-delà du centile 90, ou en deçà du centile 10, doit être l'objet d'un suivi particulier.
Histogramme
Même s'il est considéré par beaucoup comme une représentation graphique, et qu'il a donc plus sa place dans une description des méthodes de Visualisation des données, l'histogramme est un chaînon naturel entre une représentation exhaustive des données et la description par comparaison à des lois statistiques connues.
Distribution empirique
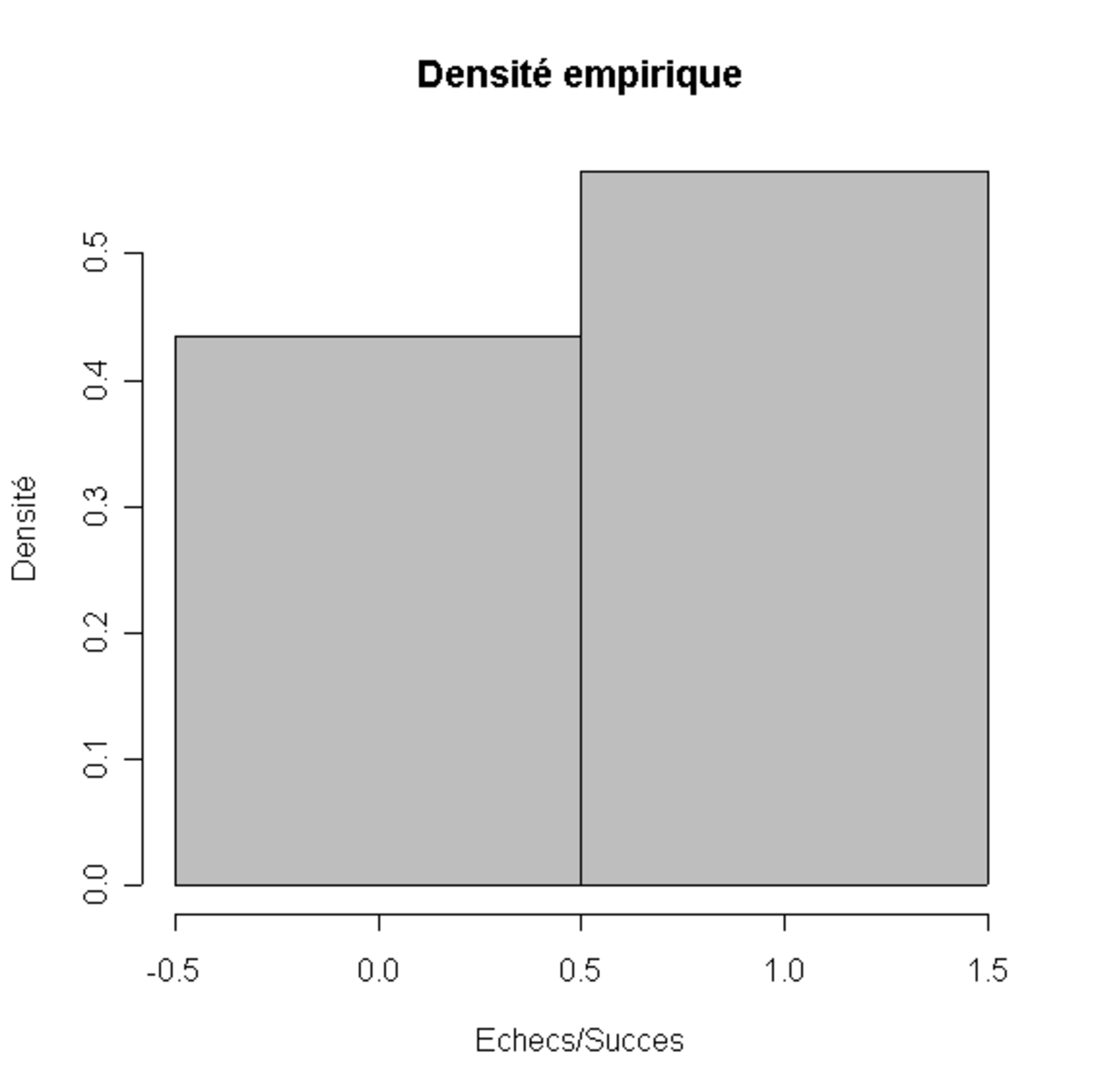
La densité empirique d'une variable à valeurs discrètes est simplement constituée de la proportion des observations prenant chaque valeur.
Si on reprend l'exemple des sportifs, la densité empirique de notre population est 57% de succès et 43% d'échecs. L'histogramme associé est très simple (cf image à gauche).
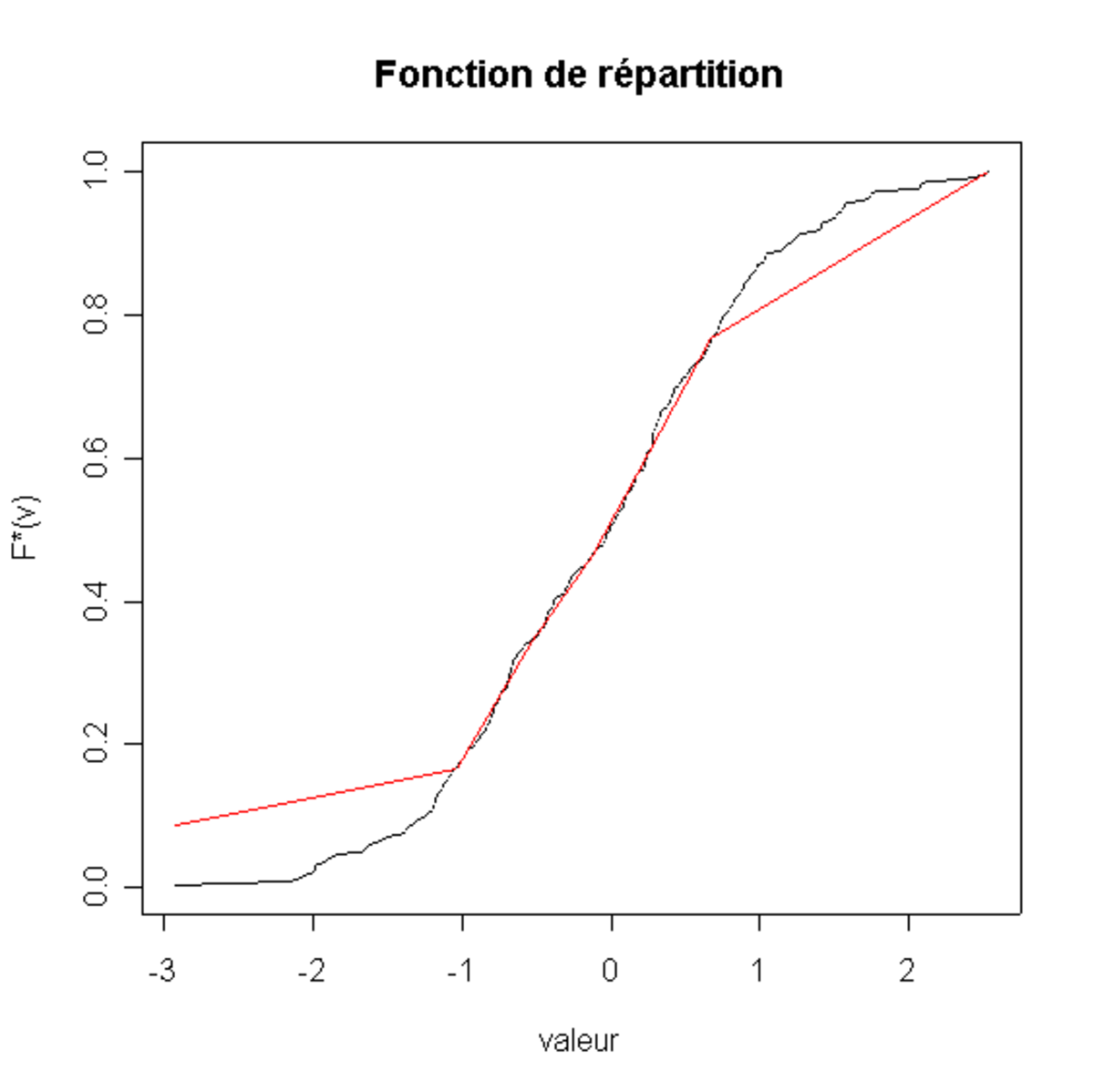
On appelle fonction de répartition empirique associée une série d'observations à valeur réelles ayant les valeurs
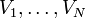
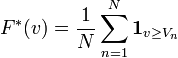
Elle est une estimation de la probabilité que la valeur d'un événement du phénomène observé ait une valeur supérieure ou égale à v.
Si on voulait en déduire la densité empirique associée aux observations, il faudrait dériver F * (v). Étant donné que la dérivée d'une indicatrice (
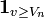
Plusieurs alternatives sont possibles:
- utiliser un estimateur par noyaux, il s'agit d'implémenter la densité suivante:
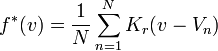
- approximer la densité par une fonction en escalier.
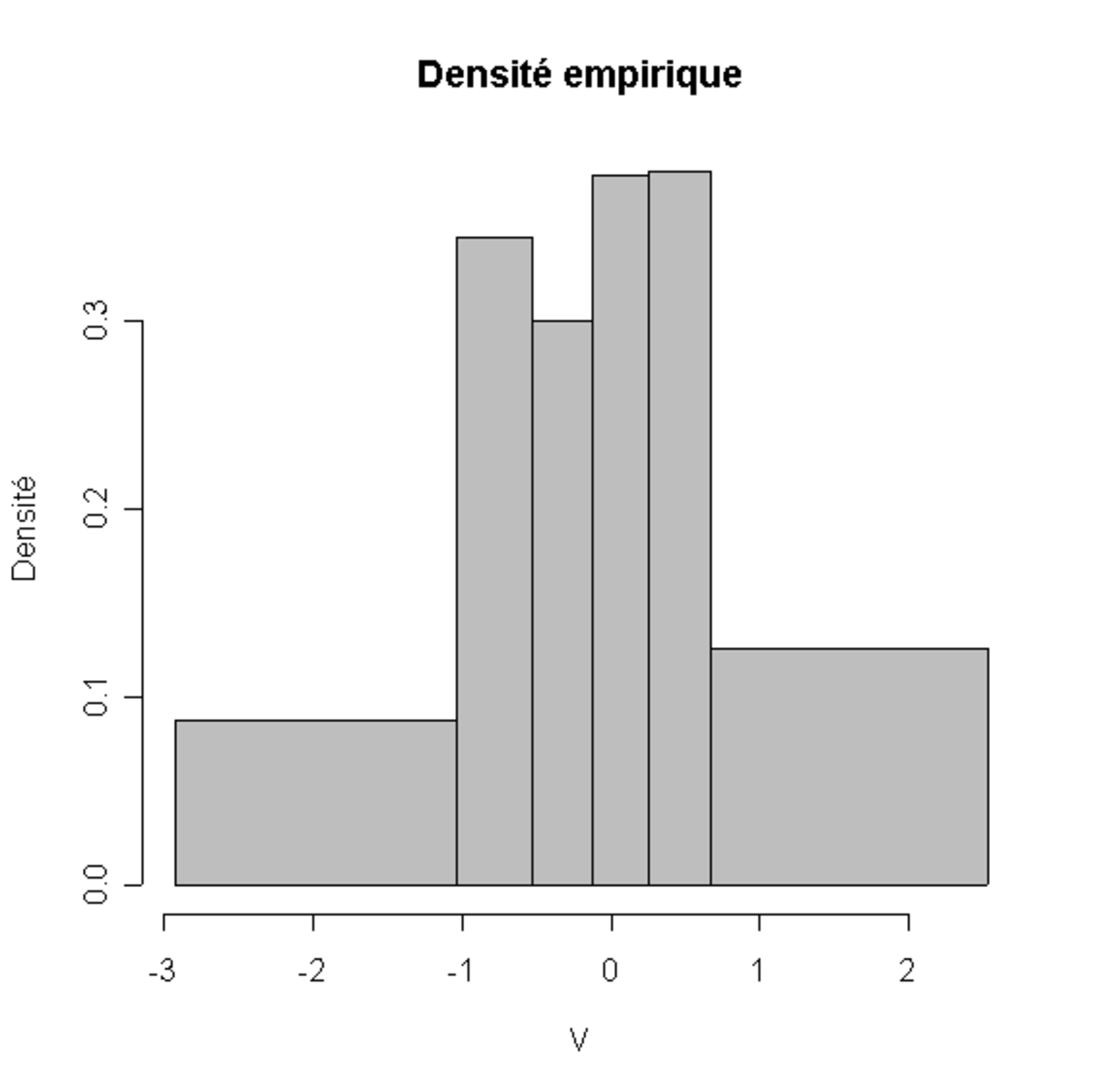
Un histogramme est la meilleure estimation par une fonction en escalier de la densité empirique. C'est-à-dire que l'intégrale de l'histogramme doit être la plus proche possible de F * (v). Remarquons que l'intégrale de l'histogramme est une fonction continue affine par morceaux. D'un certain point de vue:
- trouver la fonction continue affine par morceaux qui approxime le mieux la fonction de répartition empirique revient à caractériser totalement l'histogramme.
Dans ce cadre, le nombre de morceaux (de classes ou de barres) est un paramètre très important. Il faut recourir à un critère supplémentaire si on veut trouver sa meilleure valeur possible. On prend par exemple un critère à la Akaike ou le critère BIC (Bayesian Information Criterion); il est aussi possible de recourir à un critère d'information ou d'entropie.
Par construction, les barres de l'histogramme ne sont donc pas nécessairement toutes de la même largeur.
Construction d'un histogramme
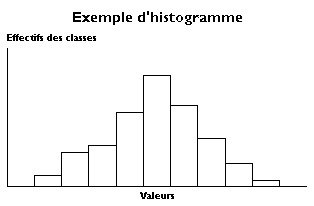
L'histogramme est une des nombreuses représentations graphiques de données statistiques possibles. Comme les quantiles, l'histogramme découpe la population en classes mais le point de vue est différent.
Avec les quantiles, le but est de localiser les frontières entre classes de même effectif. Ils sont souvent utilisés, par exemple en matière de revenus, pour comparer les deux classes extrêmes.
Pour les histogrammes, les largeurs de classes sont choisies afin de rendre le mieux possible compte de la distribution réelle des observations. Il s'agit d'une tâche difficile.
Pour plus de simplicité, les classes des histogrammes sont parfois pris de même largeur et de hauteur variable : on appelle de tels histogrammes des diagrammes en barres. Ce ne sont pas de véritables histogrammes.
Il est possible de comparer la distance entre ces deux courbes.
- par exemple en utilisant le Test de Kolmogorov-Smirnov
- où en remarquant que la distance entre ces deux courbes (définie par la surface entre elles) suit une loi du Χ2.
En allant plus loin, ce genre de méthode de comparaison de fonctions de distribution (ici entre celles issues de l'histogramme et la distribution empirique) peut être utilisé pour comparer la répartition empirique de nos observations à celle d'une loi connue (c'est par exemple le principe de la Droite de Henry). Cela permet de répondre à la question ma répartition ressemble-t-elle à une distribution connue ?.
Description par comparaison d'une distribution d'observations
Il s'agit de comparer la distribution d'observations à une loi statistique connue.
Si on identifie une loi connue (par exemple une gaussienne) dont la répartition est statistiquement indiscernable de notre distribution empirique, nous avons un très bon moyen de résumer l'information : qu'y a-t-il de plus descriptif qu'une phrase du genre mes observations sont réparties comme une loi normale de moyenne 0 et d'écart type 0.2 ?