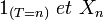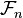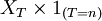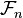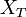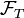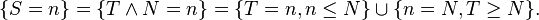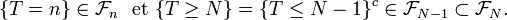Temps d'arrêt - Définition
La liste des auteurs de cet article est disponible ici.
Définitions
Définition — Une variable aléatoire
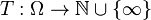
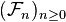
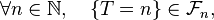
ou bien, de manière équivalente, si,
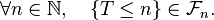
Notations
- Soient
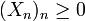
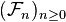
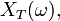
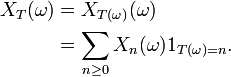
- Sur l'ensemble
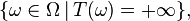
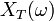
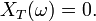
- Soit

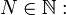
-
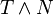
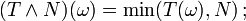
-
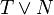
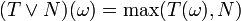
-
Interprétation
Imaginons que
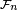
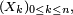
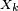
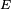
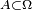
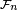
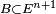
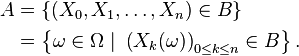
Supposons que
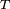
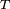

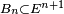
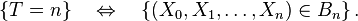
L'instant où le joueur s'arrête est donc un temps d'arrêt si la décision d'arrêt ne tient pas compte des résultats des parties futures, donc sous l'hypothèse que don de double-vue et tricherie sont exclus.
Exemples et contrexemples
Considérons une suite
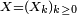
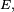
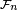
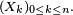
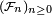
- Soit
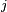
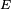
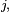
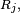

- De même pour
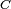
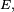
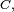
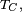
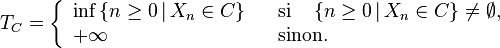
- L'instant de

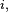
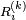

- ou encore l'instant de

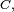
- Pour

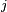
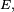
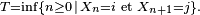
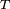
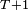
Propriétés
Propriété — Soit

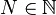
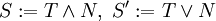
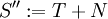
Propriété — De même, si
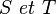
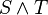
Définition et propriété — Soit

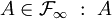

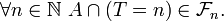
L'ensemble de ces évènements forme une sous-tribu de
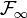

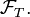
-
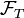
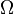
-
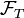
- Soit
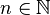
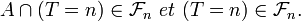
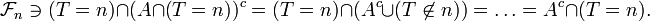
Proposition — Soient
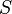

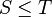
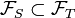
Soit
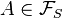
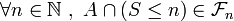
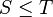
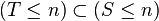
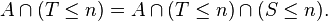
Or
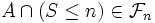
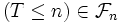

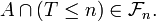
Lemme — Soit
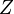
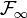
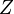
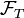
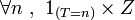
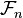
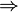
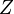
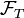
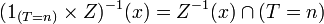
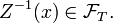
Or
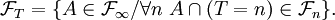
Donc
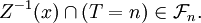
Finalement
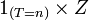
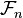
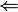
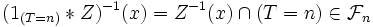
avec de plus
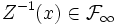
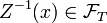
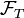
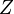
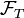
Proposition —
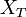
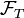
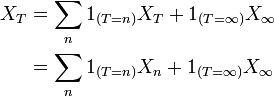
avec