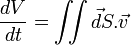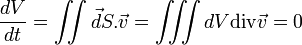Théorème de Liouville (Hamiltonien) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique, le théorème de Liouville, nommé d'après le mathématicien Joseph Liouville, est un théorème utilisé par le formalisme hamiltonien de la mécanique classique, mais aussi en mécanique quantique et en physique statistique. Ce théorème dit que le volume de l'espace des phases est constant le long des trajectoires du système, autrement dit ce volume reste constant dans le temps.
Équation de Liouville
L'équation de Liouville décrit l'évolution temporelle de la densité de probabilité ρ dans l'espace des phases. Cette densité de probabilité est définie comme la probabilité pour que l'état du système soit représenté par un point à l'intérieur du volume Γ considéré.
En mécanique classique
On utilise les coordonnées généralisées (q,p) où N est la dimension du système. La densité de probabilité est définie par la probabilité
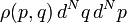
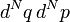
Lorsqu'on calcule l'évolution temporelle cette densité de probabilité ρ(p,q), on obtient :
![\frac{d \rho }{dt}=\frac{\partial \rho }{\partial t}+\sum_{i=1}^{N}\left[ \frac{\partial \rho }{\partial q_{i}}\dot{q}_{i}+\frac{\partial \rho }{\partial p_{i}}\dot{p}_{i}\right] = 0](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f454ff658268ee5a08ef2c0c49c6a923_309dac0b6ba6347a726be2348d9ea29b.png)
On part du fait que ρ(p,q) soit une grandeur qui se conserve lors de son déplacement dans l'espace des phases, on peut donc écrire son équation de conservation locale, c'est-à-dire pour tout élément de volume élémentaire dans l'espace des phases on a
-
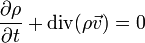
soit encore en développant
-
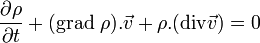
où
-
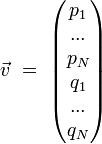
La démonstration repose sur le fait que la divergence de cette « vitesse » dans l'espace des phases est nulle, en effet :
-
![\mathrm{div} \ \vec{v} \ = \ \sum_{i=1}^N \left[ \ \frac{\partial \dot{q}_i}{\partial q_i} \ + \ \frac{\partial \dot{p}_i}{\partial p_i} \ \right]](https://static.techno-science.net/illustration/Definitions/autres/9/944d2589a394ad35f30b699118943280_0a1dbcfbbeb97d859c6216f24346c9b6.png)
![\mathrm{div} \ \vec{v} \ = \ \sum_{i=1}^N \left[ \ \frac{\partial \dot{q}_i}{\partial q_i} \ + \ \frac{\partial \dot{p}_i}{\partial p_i} \ \right]](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/944d2589a394ad35f30b699118943280_0a1dbcfbbeb97d859c6216f24346c9b6.png)
en utilisant les équations canoniques de Hamilton
- .
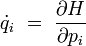
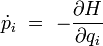
Au final, l'équation de conservation de ρ(p,q) s'écrit
-
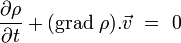
Il ne reste alors plus qu'à développer le terme
-
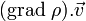
![\frac{\partial\rho}{\partial t} + \sum_{i=1}^{N}\left[ \frac{\partial \rho }{\partial q_{i}}\dot{q}_{i}+\frac{\partial \rho }{\partial p_{i}}\dot{p}_{i}\right] \ = \ 0](https://static.techno-science.net/illustration/Definitions/autres/7/76c43100877e0c875f1c0ce7de907c2a_f3f9e72e7028cd77fcfd020712986b25.png)
![\frac{\partial\rho}{\partial t} + \sum_{i=1}^{N}\left[ \frac{\partial \rho }{\partial q_{i}}\dot{q}_{i}+\frac{\partial \rho }{\partial p_{i}}\dot{p}_{i}\right] \ = \ 0](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/76c43100877e0c875f1c0ce7de907c2a_f3f9e72e7028cd77fcfd020712986b25.png)
on reconnait au final dans le terme de gauche l'expression de
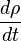
On peut utiliser les équations canoniques de Hamilton en les remplaçant dans l'équation précédente :
-
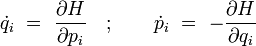
on obtient le résultat
-
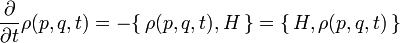
où {,} désigne les crochets de Poisson.
En mécanique quantique
D'après le principe de correspondance, on peut rapidement en déduire l'équation de Liouville en mécanique quantique :
![\frac{1}{i\hbar} [\hat H,\hat A(t)] = \left\{ \hat H,\hat A \right\} + O(\hbar^2)](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/f91903673ad0d4fef3d0b824bc3a91c6_6d46c3e217dec4de73115826165e3b25.png)
d'où on déduit :
![\frac{\partial}{\partial t}\hat \rho=\frac{i}{\hbar}[\hat\rho,\hat H]](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/5c89b1ce19809939cd2f2a3f5d991541_a361374e78a52bca44b0e1ceeb53d323.png)
Ici,
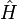
Théorème de Liouville
De l'équation de Liouville plut haut, on déduit le théorème de Liouville, qui peut s'énoncer comme suit
Théorème de Liouville — La fonction de distribution est constante le long de n'importe quelle trajectoire de l'espace des phases
ou encore sous la forme
Théorème de Liouville — Le volume d'une région de l'espace des phases reste constant lorsqu'on suit cette région dans le temps
Cela revient à dire le volume V de l'espace des phases est invariant par rapport au temps :
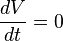
où
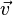
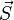
et à l'aide du théorème de Green-Ostrogradski, on trouve
car divergence du vecteur « vitesse » est nul.
