Théorème de Riesz - Définition
La liste des auteurs de cet article est disponible ici.
Contre-exemples sur d'autres corps
La droite réelle est un espace vectoriel rationnel de dimension infinie et normé par la valeur absolue usuelle, mais sa boule unité fermée est compacte, toute partie bornée est relativement compacte et l'ensemble est localement compact.
Inversement, le corps des rationnels constitue un espace vectoriel de dimension 1 sur lui-même mais aucun voisinage de l'origine n'est compact.
L'espace des suites à valeurs dans le corps fini
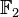
Généralisation aux espaces vectoriels topologiques
Si E est seulement un espace vectoriel topologique (sur R ou C) séparé, on a encore : E est localement compact si et seulement s'il est de dimension finie, et la démonstration est la même (en remplaçant, dans la preuve de la réciproque utilisant la propriété de Borel-Lebesgue, la boule unité B par un ouvert relativement compact contenant le vecteur nul).

















































