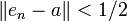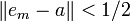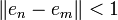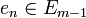Théorème de Riesz - Définition

Introduction

En mathématiques, et plus particulièrement en théorie des espaces vectoriels normés réels ou complexes, le théorème de Riesz établit un lien entre la notion de compacité, une propriété topologique, et celle de dimension, une notion algébrique. Il est nommé ainsi en l'honneur du mathématicien Frigyes Riesz.

Énoncé

Plus précisément, le théorème de Riesz s'énonce de la façon suivante :

Théorème

Soit E un espace vectoriel normé réel ou complexe. Les quatre propositions suivantes sont équivalentes :

1. E est de dimension finie.
2. Toute partie bornée de E est relativement compacte (c'est-à-dire d'adhérence compacte)
3. La boule unité fermée de E est compacte.
4. E est localement compact.

Démonstration

Sens direct

Dans ce sens, il s'agit d'un corollaire du théorème de Borel-Lebesgue : tout fermé borné dans Rⁿ est compact. Or si E est de dimension n il s'identifie à Rⁿ (ce fait est détaillé dans l'article Topologie d'un espace vectoriel de dimension finie).

Sens réciproque

En utilisant la propriété de Borel-Lebesgue

Pour la réciproque, il est commode d'utiliser la caractérisation des compacts de Borel-Lebesgue.

En effet, en notant B la boule unité de E, on a . Donc si est compacte, elle est recouverte par un nombre fini de boules de rayon 1/2 :

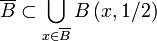
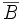
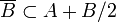
où A est l'ensemble (fini) des centres de ces boules.

Soit alors F le sous-espace vectoriel de E engendré par cet ensemble fini A. Montrons que B est incluse dans F.

De on déduit (en multipliant par 1/2) : , d'où (en remplaçant cette expression de B/2 dans la première inclusion) . Par récurrence, on démontre ainsi pour tout entier ,

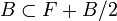
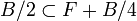
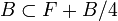
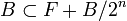
Soit alors , pour tout entier , il existe tel que . Donc , si bien que

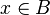
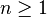
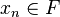
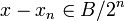
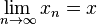
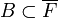
Mais F est un espace vectoriel (réel ou complexe) de dimension finie, donc est fermé : donc  : E est de dimension finie.

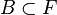
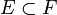
Sans utiliser la propriété de Borel-Lebesgue

Dans le cas d'un espace métrique on peut définir la compacité par la propriété de Bolzano-Weierstrass, donnons une démonstration de la réciproque plus élémentaire.

Propos heuristiques

On considère un espace vectoriel E de dimension infinie. Typiquement, on prend , le -espace vectoriel des suites (infinies dénombrables) de nombres réels.

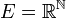
On cherche dans cet espace E une suite (x_n) qui n'admette aucune sous-suite convergente, c'est-à-dire qui contredise la propriété de Bolzano-Weierstrass, et qui ainsi démontre que notre espace E n'est pas compact.

La première suite qui vient à l'esprit, c'est la base canonique de E, c'est-à-dire la base formée des vecteurs , où le 1 est à la i-ième place.

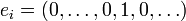
Et, effectivement, si est un espace préhilbertien réel ou complexe de dimension infinie, si est une base orthonormée de E et si est une suite injective à coefficients dans et à valeurs dans I, alors, la suite est une suite qui n'a aucune valeur d'adhérence.

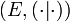
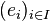
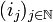
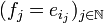
En effet, dans le cas contraire (raisonnement par l'absurde), on pourrait supposer, quitte à extraire une sous-suite que la suite (f_j)_j converge vers a.

On note tout d'abord que a est non-nul car tous les f_j sont de norme 1, donc a aussi.

Il existe donc un vecteur de base tel que est non-nul.

Pourtant, à cause du caractère orthonormé de la base qu'on a choisie, à partir d'un certain rang, est nul. C'est absurde.

 

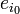
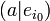
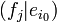
Il nous faut donc trouver l'analogue d'une base orthonormée dans un espace vectoriel E qui n'a pas de produit scalaire. Désormais, est un ou -EVN de dimension infinie.

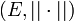
L'analogue de l'orthonormalisation de Schmidt

On se donne une famille libre . On va construire une suite (e_i) qui sera une pseudo-orthonormalisée de Schmidt de (x_i).

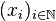
D'abord, on pose , de telle sorte que | | e₀ | | = 1.

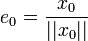
Puis, pour e₁, on procède ainsi. On note E₀ l'espace vectoriel de dimension finie engendré par e₀ ; c'est de plus un fermé de E. En particulier, il existe un point tel que . Dans le cas des espaces préhilbertiens, c'est normalement le projeté orthogonal de x₁ qui joue le rôle de y₀. S'inspirant alors de l'orthonormalisation, on pose .

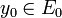
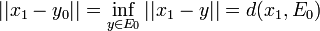
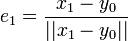
On itère ensuite la construction : E₁ est engendré par e₀ et e₁ ; y₂ réalise la distance de x₂ à E₁, etc.

La démonstration

On montre alors que la suite e_n contredit la propriété de Bolzano-Weierstrass. Par l'absurde, supposons que la suite e_n admette une valeur d'adhérence a.

Pour aboutir à une contradiction, rappelons quelques propriétés de la distance à un sous-espace vectoriel : si F est un sous-espace vectoriel de l'EVN E et si , alors, pour tout et tout λ dans ou , on a :

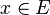
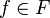
• d(x + f,F) = d(x,F)
• d(λx,F) = λd(x,F)

On a donc .

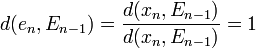
Or, par définition de ce qu'est une valeur d'adhérence, il existe deux indices n < m, tels que et . L'inégalité triangulaire donne : ce qui est absurde puisque .