Théorème de l'élément primitif - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Un exemple explicite - Énoncé du théorème - Motivation - Démonstration - Cas des corps parfaits

Démonstration

La proposition 1 implique la proposition 2

Le résultat est immédiat.

La proposition 2 implique la proposition 3

C'est une conséquence des deux dernières propositions démontrées dans le paragraphe Morphisme dans la clôture algébrique.

La proposition 3 implique la proposition 4

Supposons qu'il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3. Alors son polynôme minimal est de degré n, et K(l) est un espace vectoriel inclus dans L et de même dimension. Les deux espaces sont égaux et la proposition est démontrée. Il suffit alors de démontrer l'existence de l, ce qui est fait en fin de paragraphe.

La proposition 4 implique la proposition 1

Soit l un générateur de L. l est d'ordre n et donc il existe n morphismes de L dans Ω laissant invariant K. Soit alors r un élément quelconque de L alors L est une extension de K(r) et chaque morphisme de L est la composée d'un morphisme de K(r) étendu à L et d'un morphisme de L laissant invariant K(r). Soit n_r le nombre de morphismes de K(r) dans Ω laissant invariant K et n' le nombre de morphismes de L dans Ω laissant invariant K(r). 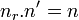Nous avons les relations : $\displaystyle n_r.n' = n$ , $n_r\le[K(r):K]$ , $n' \le[L:K(r)]$ et $\displaystyle[L:K(r)].[K(r):K]=n$ . On en conclue que $\displaystyle n_r=[L:K(r)]$ . Les images de r par les différents morphismes de K(r) dans Ω laissant invariant K sont distinctes deux à deux car sinon les morphismes seraient confondus. Le polynôme minimal de r admet donc [K(r):K] racines distinctes. Nous avons démontré que r est séparable.

Si K est un corps fini, alors il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3.

Si K est un corps fini, alors le groupe multiplicatif associé à L est un groupe cyclique. Si l est choisi parmi les éléments générateurs du groupe, alors il possède n images distinctes par les n morphismes. Sinon, il existerait des morphismes confondus. Et la proposition est démontrée.

Si K est un corps infini, alors il existe un élément l de L ayant n images distinctes par les n morphismes de la proposition 3.

Considérons V_ij l'ensemble des vecteurs de L ayant même image par le i^e et le j^e morphisme. V_ij est un sous-espace vectoriel différent de L. Une propriété des unions des espaces vectoriels montre que l'union des V_ij n'est pas égal à L. Il existe donc un élément l de L qui n'est élément d'aucun V_ij. Son polynôme minimal admet donc n racines distinctes. Ce polynôme minimal possède un degré qui divise n, d'après une propriété démontrée dans l'article Extension algébrique. Son degré est donc exactement n. l est donc générateur et séparable et la démonstration est terminée.

Note

On en trouvera une esquisse, empruntée à van der Waerden, dans l'un des liens externes proposés

Cas des corps parfaits

La séparation est une propriété relativement fréquente dans les extensions algébriques. Par exemple si le corps K est de caractéristique 0 alors toute extension est séparable. La caractéristique d'un corps est nulle si l'addition réitérée de l'unité n'est jamais nulle, donc si son sous-corps premier est $\mathbb Q$ . En conséquence, toute extension du corps des nombres rationnels ou des nombres réels est séparable. Tout corps fini ne possède, lui aussi, que des extensions algébriques séparables.