Théorème de l'élément primitif - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus spécifiquement en algèbre, le théorème de l'élément primitif est un des théorèmes de base de la théorie des extensions finies de corps.
Le théorème établit une équivalence, si l'extension est finie, entre la notion d'extension séparable, le nombre de morphismes de l'extension dans la clôture algébrique laissant invariant le corps de base et l'existence d'un élément séparable (appelé élément primitif) générant l'extension.
Ce théorème fait partie des deux piliers de la théorie de Galois dans le cas des extensions finies. Il établit une équivalence qui introduit la notion de séparabilité. Il est utilisé par exemple pour la démonstration du théorème fondamental de la théorie de Galois.
Un exemple explicite
Il est souvent facile de construire explicitement un élément primitif. Ainsi, prenons
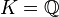
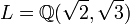
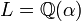
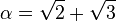
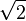
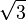
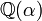
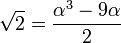
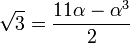
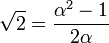
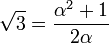
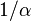
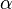
Énoncé du théorème
Soit L une extension finie de dimension n sur un corps K, et Ω la clôture algébrique de K. Alors le théorème de l'élément primitif prend la forme suivante:
-
- Les quatre conditions suivantes sont équivalentes:
- L'extension L est séparable sur K.
- L'extension est engendrée par des éléments séparables.
- Il existe exactement n morphismes de L dans Ω laissant invariant K.
- L est une extension simple générée par un élément séparable (appelé élément primitif).
Remarque: Il existe d'autres expressions du théorème de l'élément primitif, par exemple: toute extension séparable finie est simple. Une autre forme est la suivante: l'extension L est simple si et seulement si elle contient un nombre fini d'extensions de K.
Motivation
Article détaillé: Extension séparable
Une démonstration purement calculatoire de l'existence d'un élément primitif dans le cas général (même en se restreignant aux nombres algébriques) est assez délicate, et il s'avère plus efficace de se placer dans le cadre plus vaste des extensions galoisiennes.
La théorie de Galois possède comme structure fondamentale le groupe de Galois, ce groupe permet de démontrer une série de résultats géométriques, comme la caractérisation des nombres constructibles pour déterminer par exemple les polygones réguliers constructibles à la règle et au compas, la résolution d'équations algébriques ou d'établir des résultats en théorie des nombres comme le grand théorème de Fermat dans beaucoup de cas particuliers.
Comme autre exemple de ce groupe, on peut citer la caractérisation des corps finis. Le groupe permet de déterminer la structure exacte du corps ainsi que la nature des différents polynômes à coefficients dans ce corps.
Pour permettre ces démonstrations, le groupe de Galois doit être suffisamment vaste, ce qui signifie deux propriétés : l'extension doit être séparable et normale. Un élément de l'extension est dit séparable si et seulement si son polynôme minimal à coefficients dans K ne possède pas de racines multiples dans sa clôture algébrique. Une extension est dite séparable si tous ses éléments le sont. Le théorème indique qu'il suffit qu'un élément bien choisi soit séparable pour que toute l'extension le soit. Cette propriété est importante car la racine d'un polynôme est toujours transformée par un élément du groupe de Galois en une autre racine. S'il existe des racines multiples, alors le groupe devient trop petit pour que le théorème fondamental de la théorie de Galois puisse s'appliquer.
Dans le cas où l'extension est de dimension finie en tant qu'espace vectoriel sur le corps de base K, si l'extension est séparable alors le nombre de morphismes de l'extension dans la clôture algébrique est le bon. Il existe de plus une propriété forte: il existe un élément l de l'extension tel que L est égal à K(l) c’est-à-dire que L est la plus petite extension contenant K et l et bien sûr l est séparable. On parle alors d'extension simple algébrique. La réciproque est aussi vraie et est constitutive du théorème de l'élément primitif.

















































