Théorie des représentations d'un groupe fini - Définition

Introduction

Ferdinand Georg Frobenius, fondateur de la théorie de la représentation des groupes.

En mathématiques et plus précisément en théorie des groupes, la théorie des représentations d'un groupe fini est un cas particulier de représentation des groupes. Il traite du cas où le groupe étudié est d'ordre fini.

L'objectif de cette théorie est l'étude des morphismes d'un groupe fini vers GL(V) le groupe général linéaire des automorphismes d'un espace vectoriel V de dimension finie.

Cet article traite de l'aspect mathématiques, un article de synthèse existe : Représentations d'un groupe fini.

Généralité

Définitions

G désigne dans cet article un groupe fini d'ordre g. Son élément neutre est noté 1, et si s et t sont deux éléments de G la loi de composition interne du groupe sur s et t est noté st. V désigne un espace vectoriel de dimension finie notée n sur un corps noté K de caractéristique première avec g ou nulle.

• Une représentation du groupe G est la donnée d'un espace vectoriel V et d'un morphisme de groupe ρ de G vers le groupe linéaire GL(V). Une représentation est notée (V, ρ) ou parfois et abusivement V.

L'application ρ est à valeur dans l'espace des applications linéaires et préserve la loi du groupe, ce qui est équivalent aux propriétés suivantes :

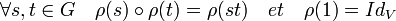
Les notations ρ(s) (v) ou ρ_s.v ou même s.v désignent l'action d'un élément s du groupe G sur un élément v de l'espace vectoriel V.

• La représentation est dite fidèle si et seulement si le morphisme ρ est injectif.

• La dimension de V est appelée degré de la représentation.

La théorie pourrait être étendue sur des espaces V de dimension quelconque, cependant, V apparaît alors comme une somme directe de représentations de dimensions finis répétées une infinité de fois. Ce cas ne représente pas d'intérêt théorique.

Remarque : Ces notations sont utilisés par défaut pour le reste de l'article.

Représentation et matrice

Soit (e_i) une base de V. La donnée de la base permet d'associer à chaque endomorphisme a de V, une matrice (a_ij) carré d'ordre n, la dimension de V. Les coefficients de la matrice sont donnés par les égalités suivantes :

L'application qui à un endormorphisme a associe la matrice définie précédemment est un isomorphisme de K-algèbre de L_K(E) l'ensemble des endormorphismes de V, dans M_n(K) l'ensemble des matrices carrés d'ordre n à coefficients dans K. Ce morphisme induit un isomorphisme de groupe de GL(V) dans l'ensemble des matrices carrés inversibles d'ordre n, c’est-à-dire des matrices de déterminant différent de zéro.

Notons R_s la matrice de ρ_s, on a alors les deux propriétés suivantes :

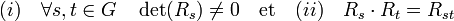
Réciproquement, la donnée des matrices R_s et de la base définit une représentation linéaire de G dans V :

• Une représentation sous forme matricielle du groupe G de degré n est la donnée d'une application de G dans M_n(K) tel que les images vérifient les égalités (i) et (ii).

Morphisme de représentation

Soit (V, ρ) et (V' ,ρ') deux représentations du groupe G:

• Un morphisme de représentation de (V, ρ) dans (V' ,ρ') est une application linéaire θ de V dans V' vérifiant la propriété suivante :

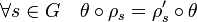
Un cas important est celui où θ est un isomorphisme, il donne lieu à la définition suivante :

• Les représentations (V, ρ) et (V' ,ρ') sont dites isomorphes ou semblables si et seulement s'il existe un isomorphisme τ de V dans V' vérifiant les égalités suivantes :

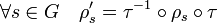
Cette définition se traduit en termes de représentations sous forme matricielle. Deux représentations matricielles R et R' sont dites isomorphes si et seulement s'il existe une matrice carrée P d'ordre n inversible tel que :

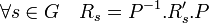
Il est possible, sans perte de généralité d'identifier deux représentations isomorphes. En particulier, deux représentations isomorphes possèdent le même degré.

• Les représentations (V, ρ) et (V' ,ρ') sont dites disjointes si et seulement si elle n'ont aucune composantes irréductibles communes, ou encore s'il n'existe aucun morphisme entre les deux représentations autre que le morphisme nul.