Théorie des représentations d'un groupe fini - Définition

Caractère

Les caractères représentent un des aspects les plus essentiels de la théorie.

Lemme de Schur

Un aspect important de la théorie des représentations d'un groupe fini, est celui du caractère d'une représentation :

• Le caractère χ_ρ de la représentation (V, ρ) est une application de G dans K qui à s associe la trace de ρ_s.

Cette notion, dans de nombreux cas, caractérise la représentation. La proposition suivante en est un exemple :

• Les caractères de deux représentations isomorphes sont égaux.

Comme toute représentation est somme directe de représentations irréductibles, la définition suivante prend tout son sens :

• Un caractère associé à une représentation irréductible est dit caractère irréductible.

Supposons que K soit égal à le corps des nombres complexes. Un caractère est alors un élément de . Cet espace est muni du produit hermitien défini dans le paragraphe Produit scalaire. Le lemme de Schur permet de démontrer que :

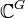
• La famille des caractères irréductibles est orthonormale.

La dernière proposition reste vraie si l'ordre du groupe g est première avec la caractéristique du corps et si le polynôme X^g - 1 est scindé dans le corps. La théorie de Galois garantit qu'une telle extension existe toujours. Dans le cas d'un corps fini l'extension reste un corps fini.

Représentation régulière

Une représentation particulière permet d'obtenir un représentant de chaque représentation irréductible, c'est la représentation régulière :

• Soit V un espace vectoriel de dimension g et (e_s) une base de V indexé par G. Soit ρ le morphisme de groupe de G dans GL(V), qui à u un élément de G associe ρ_u l'automorphisme de V qui a pour image du vecteur e_s le vecteur e_t avec t = u.s. Alors la représentation (V, ρ) est appelée représentation régulière de G.

Si (V_i, ρ_i) quand i varie de 1 à h est la famille des représentations irréductibles de G et d_i la dimension de V_i, alors la représentation régulière contient exactement d_i copies de la représentation (V_i, ρ_i). On obtient l'égalité :

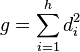
Fonction centrale

Un sous-espace vectoriel de K^G est important, il correspond à l'ensemble des fonctions centrales.

• Une application définie sur G est dite fonction centrale si et seulement si elle est constante sur chaque classe de conjugaison.

Les propriétés des traces montrent que le caractère d'une représentation est une fonction centrale, de plus :

• Les caractères irréductibles forment une base orthonormale des fonctions centrales à valeur dans le corps des nombres complexes.

On en déduit que le nombre de représentations irréductibles est égal au nombre de classes de conjugaison du groupe.

Dans le cas où K est de caractéristique nulle, alors si le corps de décomposition du polynôme X^g - 1 est inclus dans K, les résultats précédents s'appliquent. Dans le cas où K est de caractéristique p non nulle, alors si p est premier avec g et si K est algébrique les résultats s'appliquent encore.

Extension

Motivation

Un objectif important de la théorie des groupes finis est la classification. Elle se fonde sur deux concepts : un ensemble de briques élémentaires correspondant à des groupes finis facilement analysable et une extension qui permet, à l'aide des briques élémentaires de construire les groupes de la famille.

Dans le cas des groupes abéliens, les briques élémentaires sont constituées par les groupes cycliques, l'extension est celle du produit direct. Ainsi tout groupe abélien fini est produit direct de groupes cycliques.

Dans le cas général, les briques élémentaires sont les groupes simples et l'extension les produits directs et semi-directs.

Il est donc naturel de traduire en termes de représentations les deux grandes méthodes d'extension.

Produit tensoriel

Le produit tensoriel est compatible avec les représentations, ce qui signifie que l'on peut définir le produit tensoriel de deux représentations. On peut donc obtenir une représentation à l'aide de deux représentations d'un groupe, ou encore une représentation à l'aide de deux représentations de deux groupes distincts.

Dans le deuxième cas, on obtient une représentation du groupe produit. Cette méthode respecte les représentations irréductibles. L'application produit tensoriel des représentations irréductibles des deux groupes est à valeur dans les représentations irréductibles du groupe produit. De plus, cette application est bijective. C’est-à-dire qu'un groupe contenant deux sous-groupes dont il est le produit direct a pour caractère irréductibles des produits de caractères irréductibles des représentations des sous-groupes.

Le caractère du produit tensoriel deux deux représentations est le produit des deux caractères.

On peut enfin noter qu'il existe deux sous-espaces naturellement invariant dans le produit tensoriel de deux espaces, ceux correspondant aux formes bilinéaires symétriques et ceux aux formes alternées.

Les démonstrations (présentes dans l'article associé) se fondent essentiellement sur les propriétés des caractères.

Représentation induite

Une représentation induite est un mode de construction d'une représentation d'un groupe G à l'aide d'un de ses sous-groupes H. Soit (W, θ) une représentation de H, une représentation (V, ρ) est dite induite par celle de (W, θ) si et seulement si les différents sous-espaces ρ_cW où les valeurs de c forment un système de représentants des classes à gauche de G/H, sont, en somme directe, égale à V.

Il existe une unique représentation induite de G par une représentation (W, θ) d'un sous-groupe H. En termes de G-module, la représentation induite s'exprime simplement :

Elle correspond à une extension des scalaires K[H] à l'anneau K[G] sur le H-module W.

Dans le cas où H est un sous-groupe normal de G, la représentation induite est équivalente à un produit semi-direct. La technique de la représentation induite est largement utilisée en théorie des groupes finis, par exemple pour la caractérisation des groupes simples.

Les représentations induites sont le cadre de nombreux théorèmes. On peut citer l'un des plus anciens : la formule de réciprocité de Frobenius Si ψ désigne le caractère de la représentation θ de H et χ celui d'une représentation de G, si Ind ψ désigne le caractère d'une représentation induite et Res χ le caractère de la restriction de ρ à H, alors :