Théorie des représentations d'un groupe fini - Définition

Exemples

Groupe symétrique d'indice trois

Le groupe symétrique S₃ d'indice trois est un groupe de six éléments constitué des permutations d'un ensemble {e₁, e₂, e₃}. L'ensemble des combinaisons linéaires formelles sur le corps des réels de la famille (e₁, e₂, e₃) est un S₃-module que l'on note V.

Le groupe S₃ est engendré par les trois transpositions : t₁ défini par t₁(e₂) = e₃, t₂ défini par t₂(e₁) = e₃ et t₃ défini par t₃(e₁) = e₂. Si la représentation est notée (V, ρ) et la matrice de permutation de ρ(t_i) dans la base canonique M_i, alors :

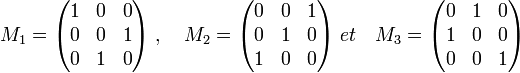
On remarque l'existence de deux espaces stables pour les trois transpositions et donc pour le groupe entier, l'un est engendré par e₁ + e₂ + e₃ et l'autre par les deux vecteurs e₁ - e₂ et e₁ - e₃. V apparait comme la somme directe de deux sous-espaces vectoriel V₁ de dimension un et V₂ de dimension deux. Si ρ₂ le morphisme de groupe de S₃ dans GL(V₂) qui à g élément de G associe la restriction de ρ(g) à V₂, alors (V₂, ρ₂) est une autre représentation du groupe. La restriction de ρ(g) à V₂ est bien un automorphisme car V₂ est stable par ρ(g). On remarque de plus que (V₂, ρ₂) tout comme (V, ρ) est une représentation fidèle.

On remarque enfin, que si V est muni du produit scalaire canonique, les images du groupe G sont des isométries. Il est donc judicieux de choisir comme base de V₂ une base orthonormée, par exemple :

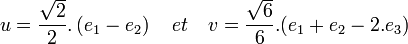
Si N_i désigne la matrice de ρ₂(t_i) dans la base (u, v), on obtient :

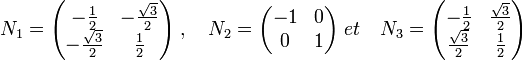
La représentation ρ₂ est fidèle et, parmi celles vérifiant cette propriété, de plus petit degré. En effet, toute représentation de degré un a pour image de G un groupe abélien alors que S₃ ne l'est pas. On démontre que toute représentation fidèle de degré deux est isomorphe à celle là.

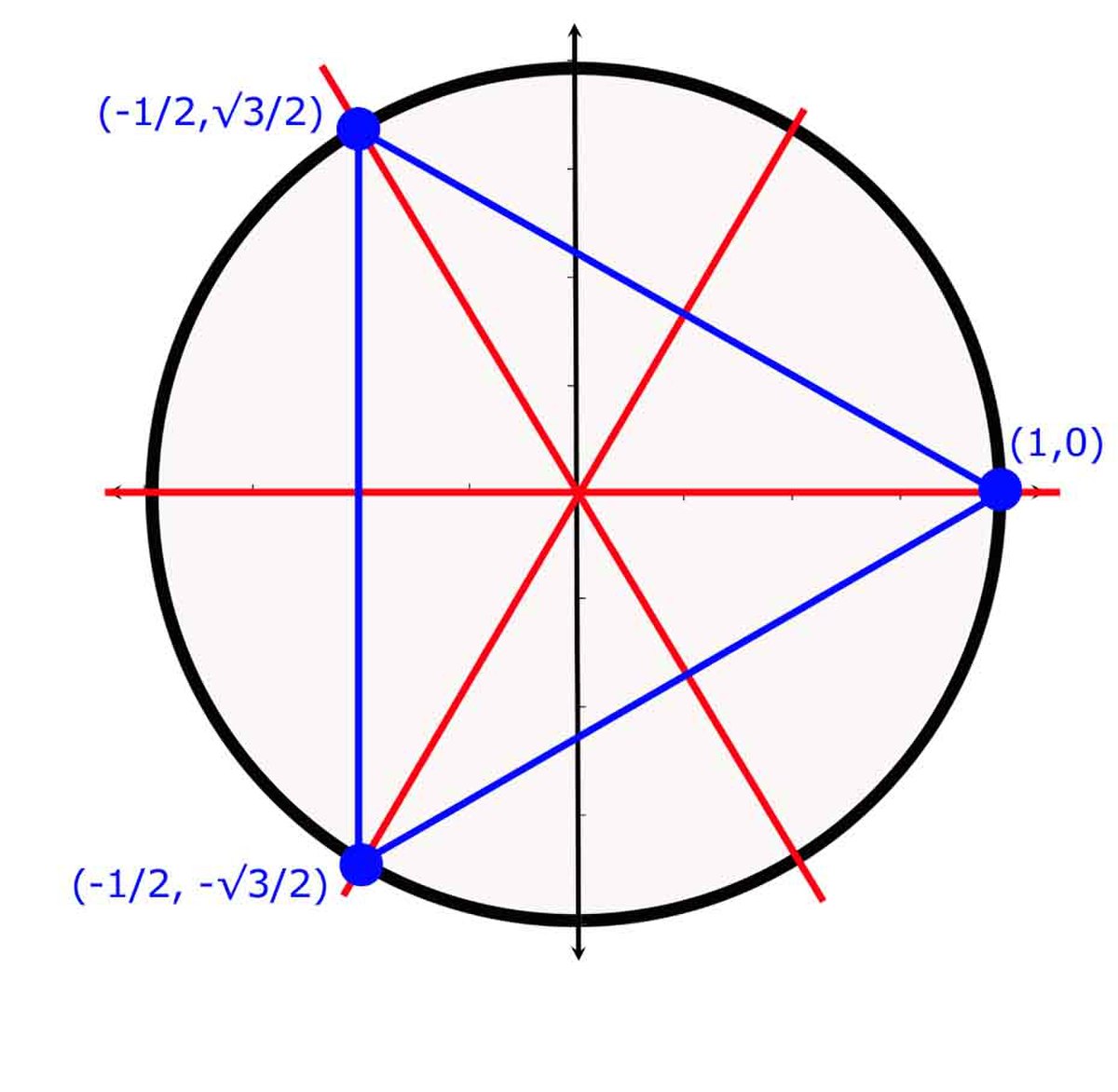
La figure de droite illustre une interprétation graphique de la représentation. Les lignes rouges représentent les trois axes de symétrie des trois transpositions. On remarque que le triangle est invariant par les transpositions et donc par le groupe entier. Réciproquement, toute isométrie laissant invariant le triangle est élément du groupe.

Exemples généraux

• Si G est un sous-groupe de GL_n(K), G agit naturellement sur Kⁿ. La représentation associée est appelée représentation standard.

• Si l'espace vectoriel V de la représentation est de dimension un, il est possible de l'identifier à K. Si de plus G est un groupe d'ordre fini n , on remarque que si g est un élément du groupe, ρ(g)ⁿ est égal à l'unité. Ce résultat est une conséquence du théorème de Lagrange. La représentation ρ prend donc ses valeurs dans le groupe des racines de l'unité de K. Une représentation d'un groupe fini dans K est appelée représentation unité.

• G agit sur lui-même par multiplication à gauche ; ceci définit une représentation sur K[G]. La représentation associée est appelée représentation régulière.

• De manière plus générale, si G opère sur un ensemble fini E = {e₁,..., e_n}, alors l'espace vectoriel V des combinaisons linéaires formelles de E sur K forme une représentation ρ définie par la formule suivante :

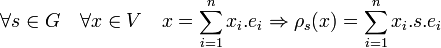
Algèbre d'un groupe

Structure semi-simple

La théorie des représentations se fonde sur deux approches, qui, sous des angles différents, permet l'analyse des représentations d'un groupe. La première est couverte par le paragraphe précédent, les caractères, la deuxième se fonde sur des structures : celle d'algèbre et de module. Une des raisons de la richesse de la théorie est la complémentarité de ces deux points de vue bien distincts.

Le groupe peut être linéarisé, c’est-à-dire que les éléments de G sont utilisés pour indexer une base (e_s) où s parcourt G, d'un K espace vectoriel. Le prolongement par linéarité permet de définir une multiplication interne :

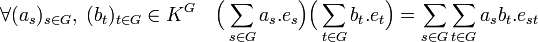
La structure obtenue est celle d'une algèbre associative sur un corps commutatif K. Elle est appelée algèbre du groupe G et est noté K[G]. Elle correspond à la représentation régulière, le contexte opératoire est néanmoins enrichi. Une algèbre simple correspond à une sous-algèbre dont les seuls idéaux bilatères (c’est-à-dire à idéal à droite et à gauche) sont l'ensemble nul et la sous-algèbre elle même. Cette notion correspond à celle de l'irréductibilité pour les représentations. Dans ce contexte, le théorème de Mascke s'énonce un peu différemment, il exprime ici que tout idéal bilatère de l'algèbre est facteur direct, c’est-à-dire qu'il possède un idéal bilatère supplémentaire. Une telle structure prend le nom d'algèbre semi-simple.

Elle permet d'interpréter différemment une représentation (V, ρ). Le morphisme ρ de G dans GL(V) peut être prolongé par linéarité sur K[G]. L'espace vectoriel est alors enrichi d'une structure de module sur l'anneau K[G]. Une telle structure prend le nom de G-module. Il existe une équivalence stricte entre les notions de représentation et celle de G-module. Les sous-modules correspondent exactement aux sous-espaces invariant par ρ. Un sous-espace irréductible prend ici le nom de sous-module simple. Avec les mêmes définitions que pour le cas de l'algèbre, le théorème de Maschke démontre que tout sous-module est un facteur direct, on parle alors de module semi-simple.

En dimension fini, une algèbre semi-simple, ainsi qu'un module semi-simple est somme directe de structures simples.

Théorème d'Artin-Wedderburn

La théorie des algèbres semi-simple est vaste et dispose de nombreux théorèmes. Le plus fondamental est probablement celui d'Artin-Wedderburn. Si K possède de bonnes propriétés, celles décrite dans le paragraphe sur les caractères, alors K[G] est somme directe de sous-algèbres isomorphes à L_K(S_i) l'ensemble des endomorphismes d'un espace vectoriel sur K nommé ici S_i et de dimension finie.

Les espaces vectoriel S_i correspondent à une famille maximale de sous-espaces irréductibles pour la représentation régulière non isomorphe deux à deux. Sous cet angle, l'égalité entre l'ordre du groupe et les degrés des représentations irréductibles s'éclaire sous un jour nouveau.

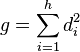
Les carrés s'interprètent comme les dimensions d'algèbres d'endomorphismes. Les composantes isotypiques correspondent à ces espaces. Ce premier résultat permet de démontrer que les composantes isotypiques forment une unique décomposition en sous-représentations à la différence d'une somme directe de représentations irréductibles.

Conséquences du théorème

L'utilisation du nouvel axe d'analyse comporte de nombreuses conséquences. On peut les classifier en trois parties :

La vision apportée par les caractères est enrichie. Un exemple est celui des fonctions centrales. Un ensemble révélateur de la structure est le centre de K[G], c’est-à-dire l'ensemble des éléments qui commutent avec toute l'algèbre. Il vérifie la propriété suivante :

• Soit c une classe de conjugaison et d_c la somme des éléments de la base canonique indexés par un élément de c. Le centre de K[G] est l'espace vectoriel engendré par les éléments d_c lorsque c parcourt l'ensemble des classes de conjugaison.

En conséquence si les éléments d_c sont identifiés à c, l'espace des fonctions centrales apparaît comme l'espace vectoriel dual du centre de G. Il existe un isomorphisme plus profond, respectant les structures d'algèbres :

• L'application φ défini ci-dessous, de l'espace des fonctions centrales K^C dans le centre de K[G] est un isomorphisme d'algèbre sur K.

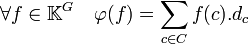
Ce résultat permet, par exemple de démontrer l'importante loi de réciprocité de Frobenius.

Le centre de l'algèbre est un anneau commutatif contenant K, cette configuration permet d'utiliser les théorèmes d'arithmétique et particulièrement ceux sur les entiers algébriques. Cette approche est à la base de la démonstration du fait que le degré de toute représentation irréductible divise l'ordre du groupe (cf le paragraphe Entier algébrique de l'article associé à ce paragraphe).

Enfin, les hypothèses restrictives sur le corps peuvent être retranchées sans effondrement de la théorie. Si elle devient différente, les résultats sur les algèbres semi-simples permettent néanmoins de conclure dans de nombreux cas. Cette configuration se produit si la caractéristique de K divise l'ordre du groupe où si le polynôme X^g - 1 n'est pas scindé, comme souvent pour le corps des nombres réels.