Transformation par polaires réciproques - Définition
La liste des auteurs de cet article est disponible ici.
Introduction

En mathématiques, et plus précisément en géométrie, la transformation par polaires réciproques est une transformation associant à une courbe une autre courbe, construite à l'aide des droites tangentes à la première.
Points cocycliques, quadrilatère inscrit
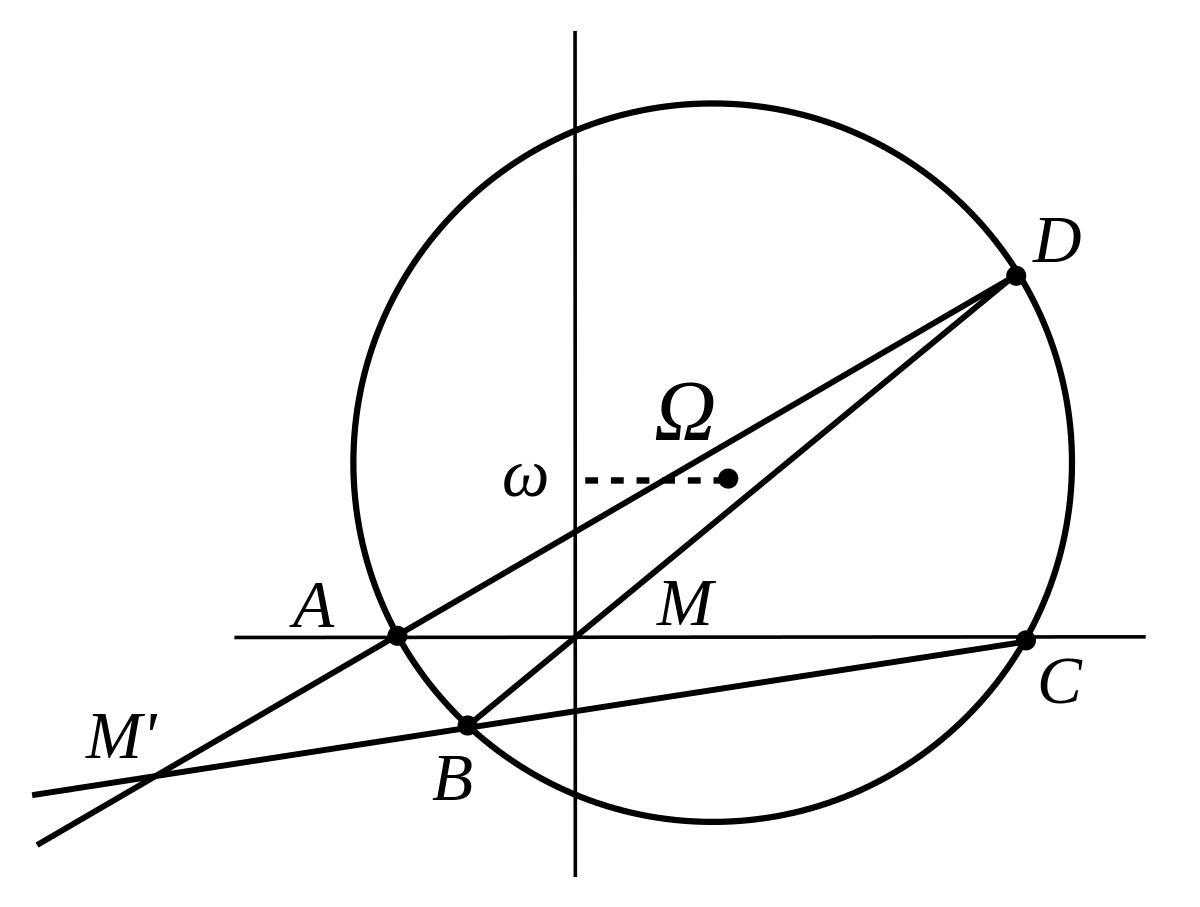
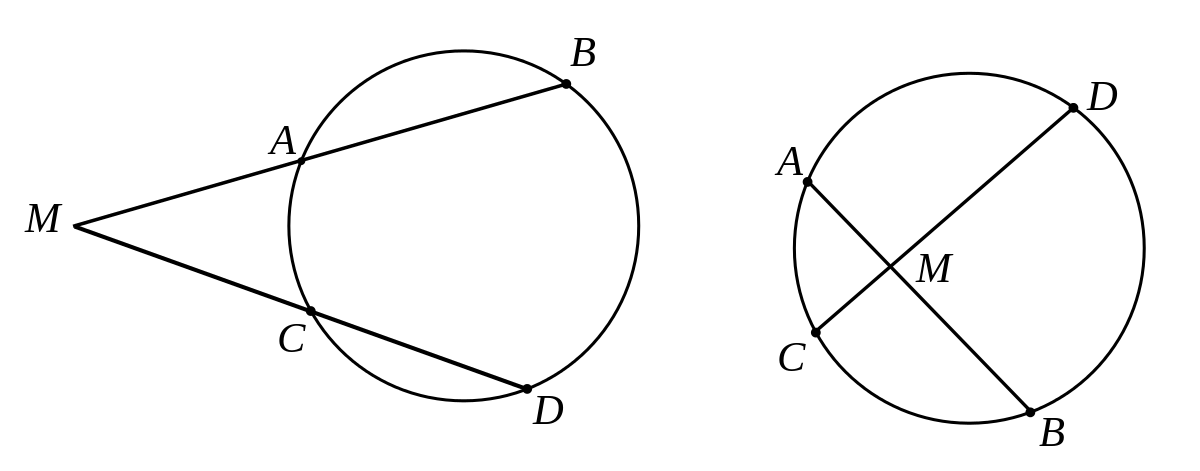
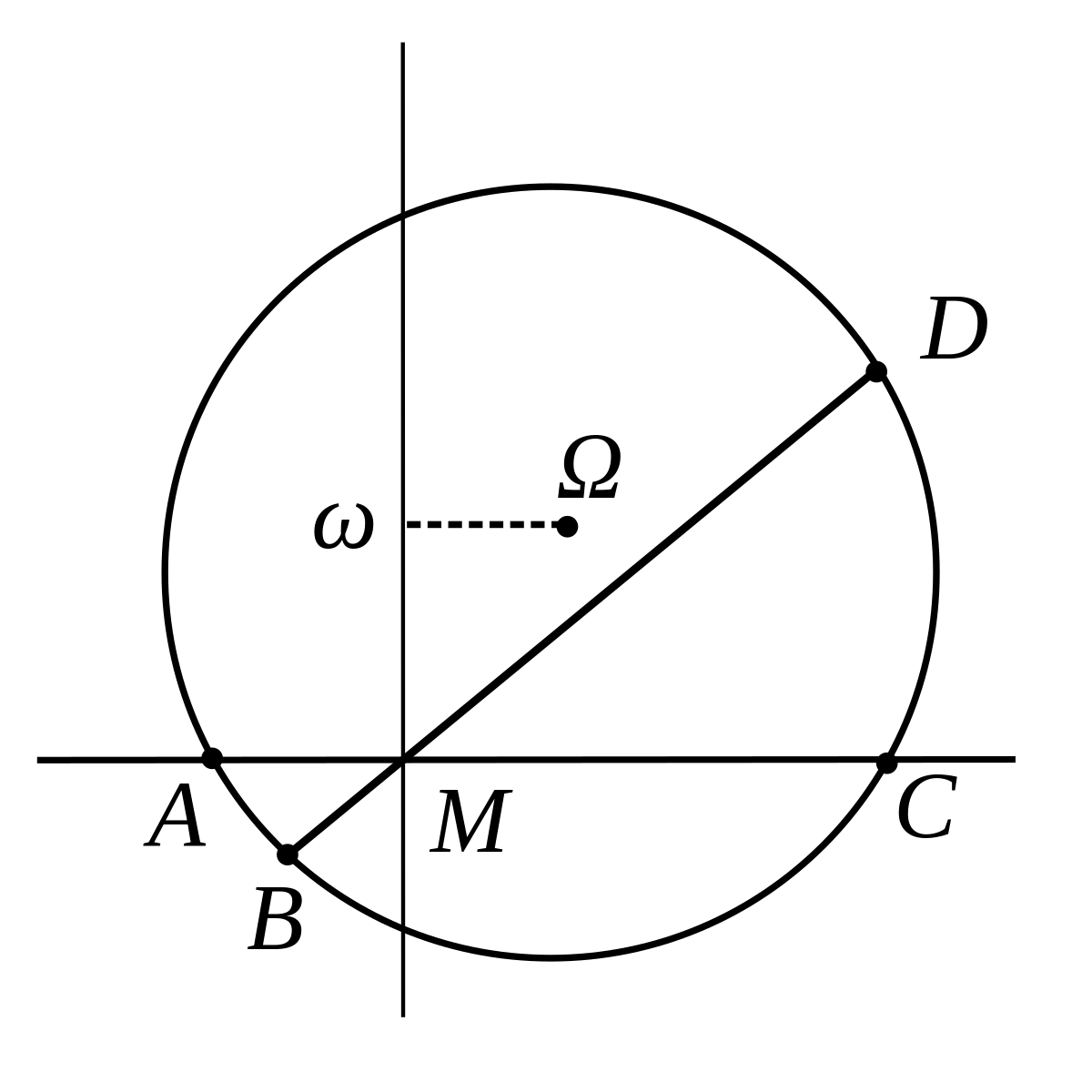
Soit A,B,C,D un quadrilatère et M l'intersection des diagonales.
Les quatre points sont cocycliques si et seulement si
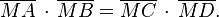
Preuve géométrique
Dans le sens direct c'est immédiat puisque c'est la puissance de M par rapport au cercle contenant les points.
Réciproquement soit

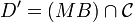
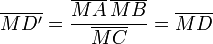
Preuve analytique
| L'origine du plan est prise en M et l'on pose A(a,0), C(c,0) sur l'axe des abscisses. Un cercle passant par A et C a pour centre
On note b,d les abscisses de B et D qui sont donc situés sur une droite Y = λX. L'équation du cercle s'écrit X2 + Y2 − (a + c)X − 2ωY + ac = 0. Remplaçant Y par λX, B et D sont sur le cercle si et seulement si b et d vérifient (1 + λ2)X2 − (a + c + 2λω)X + ac = 0 L'existence de
Mais
|
Apparition de la droite des tangentes
Soit toujours
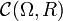

PROPRIÉTÉ : Si
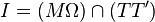
preuve analytique
On prend l'origine en M, et MΩ pour axe des abscisses. Le cercle a pour équation (X − ω)2 + Y2 = R2. Les tangentes ont pour équation Y = λX ce qui donne pour les points de contact (1 + λ2)X2 − 2ωX + ω2 − R2 = 0 équation qui admet donc une racine double (par conséquent Δ = ω2 − (ω2 − R2)(1 + λ2) = 0) qui vaut
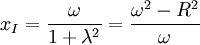
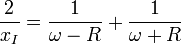
preuve géométrique
Ω étant le milieu de [AB] il suffit de prouver
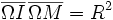
Commençons par écrire les trois triangles rectangles
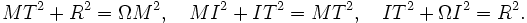
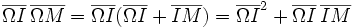
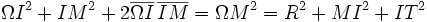
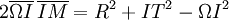
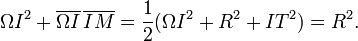
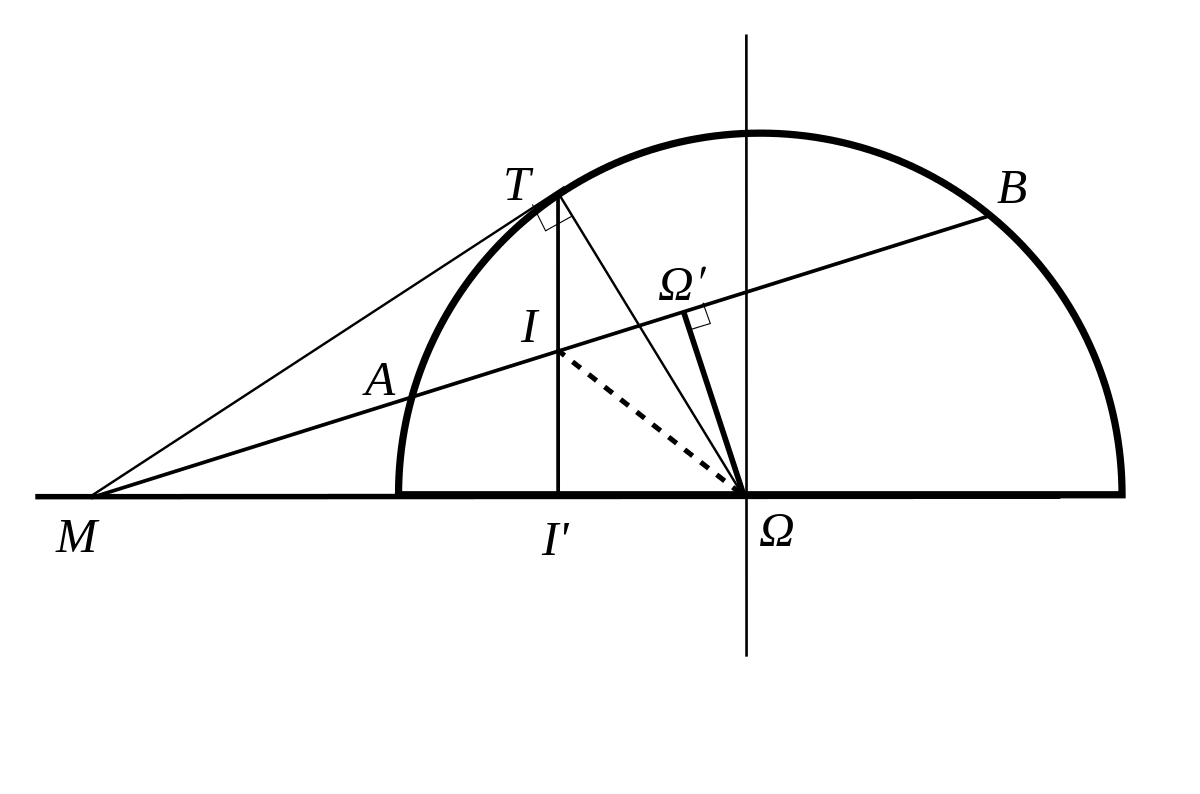
PROPRIÉTÉ : Le point d'intersection de (TT') avec toute corde issue de M divise harmoniquement la corde. [MI] divise harmoniquement [AB]
preuve géométrique
Soit I le point d'intersection de la corde avec (TT'), I' le projeté de T sur (ΩM), Ω' le projeté de Ω sur (AB).
La démonstration proposée repose à nouveau sur plusieurs triangles rectangles.
Comme Ω' est le milieu de [AB] il suffit de prouver que
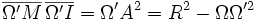
De
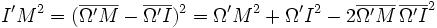
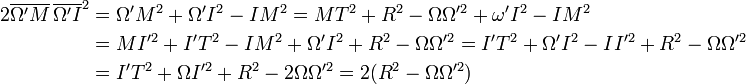
Il en résulte
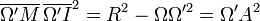
preuve analytique
On prend l'origine en M et l'on note encore A,B la corde et I le point d'intersection. La corde admet toujours une équation de la forme Y = λX si bien que
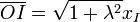
Pour prouver le résultat, il suffit de le monter pour les abcisses, c'est-à-dire :
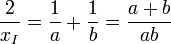
Or on a
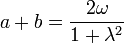
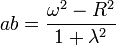
Un produit scalaire symétrique
| PROPRIÉTÉ : Notons M' l'intersection de deux des côtés du quadrilatère. On a
Preuve géométrique
en utilisant la puissance de M et M' par rapport au cercle. Mais, les points A,B,C,D étant cocycliques,
de sorte que
égalité qui résulte de la relation des sinus dans les triangles (AMD) et (ACM') puisque
Preuve analytiqueSupposons
Équation de
Équation de
Ce qui donne pour les coordonnées de M'
Comme b,d sont solutions de l'équation du second degré écrite ci-dessus, (cf. Points cocycliques-Preuve Analytique) on a
si bien que X peut aussi s'écrire
On a maintenant
Or
d'où l'on tire
On a donc finalement |
|
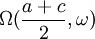
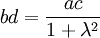
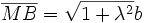
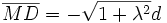


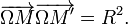
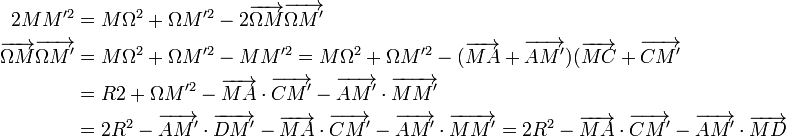
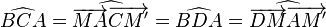
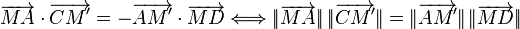
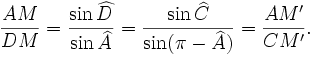
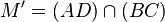
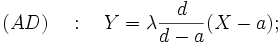
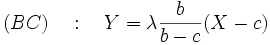
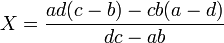
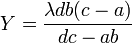
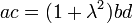
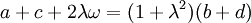
![X=\frac{bd(c-a)+ac(d-b)}{dc-ab}=\frac{bd[c-a+(1+\lambda^2)(d-b)]}{dc-ab }.](https://static.techno-science.net/illustration/Definitions/autres/e/e378450343996ec5f62258045bc0009f_dd0953702eb1fa2d80e7bccd99807e91.png)
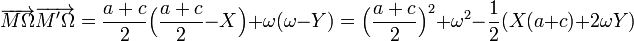
![\quad 2\omega Y=\frac{bd(c-a)}{dc-ab}[(1+\lambda^2)(b+d)-(a+c)]](https://static.techno-science.net/illustration/Definitions/autres/8/86af86816aa46bc2b726ddcf17a7a13f_a514346a3811097606cf50000085d000.png)
![\quad X(a+c)+2\omega Y=\frac{(1+\lambda^2)bd[(a+c)(d-b)+(b+d)(c-a)]}{ dc-ab}=2ac](https://static.techno-science.net/illustration/Definitions/autres/d/df6b1be482cdeaa9abed9afef9992cf4_6b31184f2b68e753767677f19e79812e.png)