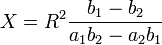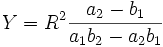Transformation par polaires réciproques - Définition
La liste des auteurs de cet article est disponible ici.
Polaire d'une courbe
Il y a deux façons naturelles de définir la polaire d'une courbe.
Ou bien à un point M de la courbe on associe sa polaire puis l'on considère l'enveloppe de ces polaires ou bien on considère le lieu formé par les pôles des tangentes à la courbe. Ces deux notions coincident.
Soit (x(t),y(t)) une courbe du plan, la tangente a pour équation Xy' − Yx' = xy' − yx' son pôle a donc pour coordonnées
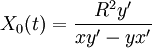
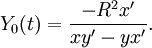
La polaire du point (x(t),y(t)) a pour équation Xx(t) + Yy(t) = R2. L'enveloppe de cette famiille de droites est déterminée par les équations
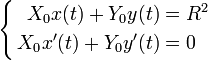
La "polarisation" échange donc les notions de point d'une courbe et de tangente à la courbe.
Polaire réciproque
Cette droite (TT') possède donc les propriétés suivantes :
- Toute corde [AB] au cercle, issue d'un point M extérieur à ce cercle, coupe cette droite en un point I tel que [MI] divise harmoniquement [AB];
- Cette droite et l'ensemble des conjugués harmoniques de M par rapport au cercle;
- Pour tout point I de cette droite, le cercle de diamètre [MI] est orthogonal au cercle de départ (cf. cerccles orthogonaux);
- Si O est le centre du cercle,
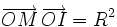
- Les intersections des diagonales de tous les quadrilatères complets issues de M sont alignés et sont sur cette droite;
- Si dans un repère centré au centre du cercle, le point M a pour coordonnées (x0,y0), l'équation de cette droite est x0X + y0Y = R2.
Définitions
Définition : Étant donné un point M et un cercle



Par conséquent si M est extérieur au cercle, c'est la droite (TT').
Réciproquement, toute droite du plan est la polaire d'un point unique nommé "pôle" de la droite.
Polaire et pôle sont reliés analytiquement par la relation : x0X + y0Y = R2 lorsque l'origine du plan est au centre du cercle.
Géométriquement, si la droite
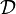
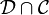

Intersection et alignement
La "polarisation" échange les notions de droites concourantes et de droite passant par deux points.
PROPRIÉTÉ Soit M1,M2 deux points (non alignés avec le centre du cercle); si D1,D2 désignent les polaires de ces points, alors
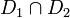
Si l'on note (xi,yi) les coordonnées de Mi, les coordonnées (x,y) de
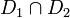
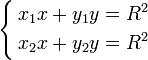
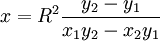
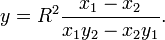
Ce point admet pour polaire la droite d'équation :
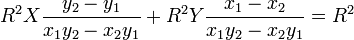
soit la droite
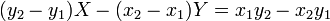
qui n'est autre que la droite (M1M2).
Géométriquement, si
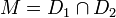

PROPRIÉTÉ Soit D1,D2 deux droites, M1,M2 leur pôles alors la droite (M1M2) est la polaire du point
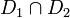
Les deux droites possèdent des équations que l'on peut mettre sous la forme a1X + b1Y = R2 et a2X + b2Y = R2
ce qui fournit les coordonnées des pôles M1(a1,b1) et M2 = (a2,b2). La droite (M1M2) a pour équation (b2 − b1)X − (a2 − a1)Y = a1b2 − a2b1
son pôle a donc pour coordonnées