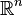Tribu (mathématiques) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Propriétés élémentaires - Motivations - Deux exemples importants : les tribus de Borel et de Lebesgue - Tribu engendrée par un ensemble de parties - Cardinalité des tribus - Constructions de tribus - Histoire du concept

Motivations

En analyse, l'importance des tribus s'est progressivement affirmée au long des trente premières années du XX^e siècle. Le siècle s'ouvre par l'élaboration par Henri Lebesgue de sa théorie de l'intégration. Dans la décennie suivante on commence à exploiter la notion géométrique de mesure en probabilités, Johann Radon construit en 1913 une théorie de l'intégration sur $\R^n$ qui généralise à la fois celle de Lebesgue et celle de Stieltjes, Felix Hausdorff définit en 1918 la mesure qui porte aujourd'hui son nom en dimensions non entières. Simultanément, on s'efforce de bâtir une axiomatisation abstraite de l'intégration dans laquelle s'intègreraient toutes ces nouvelles théories. Cette unification, réalisée dans le début des années 1930, s'appuie sur la définition moderne d'une mesure. La notion de tribu en est un élément constitutif.

Depuis la publication en 1933 des Fondements de la théorie des probabilités d'Andreï Kolmogorov, les probabilités sont solidement ancrées sur la théorie de la mesure. Les σ-algèbres y jouent un rôle incontournable, peut-être plus central qu'en analyse : ici elles ne sont pas seulement un cadre de travail, mais aussi un outil puissant. La preuve de la loi du zéro un de Kolmogorov fournit un exemple relativement élémentaire de leur efficacité.

La théorie des processus stochastiques (l'étude probabiliste de phénomènes variant avec le temps) permet de donner une interprétation intuitive de certaines tribus. Par exemple, supposons qu'on s'intéresse à l'évolution du prix d'un actif financier en fonction du temps. L'espace des événements $X$ est l'ensemble des évolutions possibles de cet actif, c'est-à-dire des fonctions associant à chaque instant un prix. 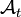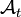Pour chaque valeur $t$ du temps, on définit ainsi une tribu $\mathcal{A}_t$ : étant donné un ensemble $A$ d'événements, on décidera que $A$ est dans $\mathcal{A}_t$ si on peut le décrire par une formulation qui, lue par un observateur vivant à la date $t$ , ne se réfère qu'au passé. 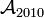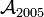Pour fixer les idées, si $A$ est l'événement « le cours de l'actif a constamment augmenté pendant l'année 2006 », il appartient à $\mathcal{A}_{2010}$ puisqu'un observateur vivant en 2010 peut en décider en consultant des archives, mais n'est pas dans $\mathcal{A}_{2005}$ (sauf à être extralucide, un observateur vivant en 2005 n'en peut rien savoir). 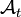On dispose finalement d'une tribu évoluant en fonction du temps, dont la valeur $\mathcal{A}_t$ représente le niveau d'information disponible à la date $t$ . Sa croissance exprime l'expansion constante de l'information disponible. Cette famille croissante de tribus (on parle de filtration) permet alors de formaliser diverses hypothèses sur le phénomène modélisé (via les concepts d'espérance conditionnelle, de martingale, etc.) puis d'en tirer mathématiquement des conclusions.

Deux exemples importants : les tribus de Borel et de Lebesgue

On appelle tribu de Borel ou tribu borélienne sur un espace topologique donné la tribu engendrée par les ensembles ouverts. Dans le cas simple et fondamental de l'espace usuel à $n$ dimensions, la tribu borélienne de $\R^n$ est engendrée par une famille dénombrable de parties, les pavés dont les sommets sont à coordonnées rationnelles. Par un résultat mentionné plus loin, elle a donc la puissance du continu — ce qui prouve incidemment qu'elle n'est pas égale à l'ensemble de toutes les parties de $\R^n$ , qui est de cardinal strictement supérieur.

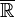
En probabilités, ou dans les théories de l'intégration dérivant de celle de la mesure, la tribu de Borel de $\R$ (ou de la droite achevée $\overline{\R}$ ) joue un rôle prééminent : c'est en effet relativement à elle qu'on définit les fonctions mesurables à valeurs réelles ou les variables aléatoires réelles.

Les tribus boréliennes sont le cadre naturel où se rencontrent les théories de l'intégration et la théorie de la mesure, notamment par le théorème de représentation de Riesz qui associe une mesure définie sur la tribu de Borel à certaines fonctionnelles sur un espace de fonctions continues.

Bien que les espaces métriques non dénombrables usuels aient des propriétés topologiques extrêmement dissemblables, toutes leurs tribus boréliennes sont indiscernables. Un théorème de Kuratowski affirme en effet que tous ceux appartenant à une très large classe, les espaces de Lusin, ont des tribus boréliennes isomorphes entre elles et en particulier isomorphes à la tribu de Borel sur la droite réelle. Les espaces de Lusin en tant qu'espaces mesurables sont donc classifiés par leur cardinal.

Sur l'espace $\mathbb R^n$ , une autre tribu mérite d'être signalée : la tribu de Lebesgue, dont les éléments sont les ensembles mesurables au sens de Lebesgue. Cette tribu contient strictement la tribu de Borel, dont elle est la complétée pour la mesure de Lebesgue. Si on accepte d'utiliser l'axiome du choix, elle ne coïncide pas non plus avec l'ensemble de toutes les parties de $\R^n$ .