Tribu (mathématiques) - Définition

Introduction

En mathématiques, une tribu ou σ-algèbre (lire sigma-algèbre) ou plus rarement corps de Borel sur un ensemble X est un ensemble non vide de parties de X, stable par passage au complémentaire et par union dénombrable (donc aussi par intersection dénombrable). Les tribus permettent de définir rigoureusement la notion d'ensemble mesurable.

Progressivement formalisées pendant le premier tiers du XX^e siècle, les tribus constituent le cadre dans lequel s'est développée la théorie de la mesure. Les exemples les plus fameux en sont les tribus boréliennes, du nom d'Émile Borel, qui construit la tribu borélienne de la droite réelle en 1898, et la tribu de Lebesgue, formée des ensembles mesurables définis par Henri Lebesgue en 1901. En conséquence, les tribus sont aussi fondamentales en théorie des probabilités, dont l'axiomatisation moderne s'appuie sur la théorie de la mesure. Dans ce domaine, les tribus ne sont pas seulement le support du formalisme, mais aussi un outil puissant, qui est à la base de la définition de concepts parmi les plus importants : espérance conditionnelle, martingales, etc.

Définition

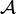
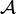
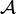
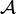
Une minorité de sources exigent également que X ne soit pas vide ; cette hypothèse supplémentaire n'est utilisée à aucun endroit de cet article.

Formellement :

1. 
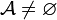
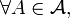
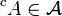
2. (où ^cA désigne le complémentaire de A dans X).
3. si alors (l'union est dite « dénombrable » parce que l'ensemble des indices l'est).

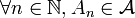
La définition qui précède a l'intérêt d'être lisible sans connaître le langage des algèbres de Boole ; si on le connaît, on peut l'exprimer sous forme plus resserrée :

Le couple est appelé espace mesurable ou espace probabilisable en fonction du contexte. Sur les espaces mesurables on définit des mesures ; sur les espaces probabilisables on s'intéresse spécifiquement aux probabilités.

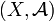
Les parties de X qui appartiennent à la tribu sont appelées ensembles mesurables. Dans un contexte probabiliste, on les appelle événements.

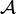
Quelques exemples

• La tribu dite triviale (aussi appelée discrète) : où représente l'ensemble de toutes les parties de X.

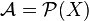
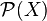
• La tribu dite grossière : .

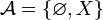
• Si X = {a,b,c,d} alors est une tribu sur X. C'est la plus petite tribu contenant l'ensemble {a}.

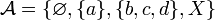
• Pour tout X, ou fini ou dénombrable est une tribu sur X.

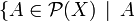
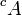
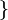
• En revanche si X est infini, ou fini n'est pas une tribu sur X, bien que ce soit une algèbre de Boole de parties de X.

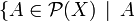
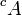
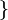
Propriétés élémentaires

• Une tribu est stable par union finie (appliquer le point 3 de la définition à une suite infinie dénombrable constituée de n ensembles, le dernier étant répété à l'infini).

• (prendre un élément et écrire ).

• ( est le complémentaire de X).

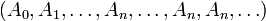
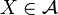
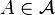
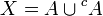
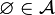
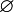
• Une tribu est également stable pour l'opération d'intersection dénombrable (d'après les points 2 et 3 de la définition) et a fortiori stable sous intersection finie :
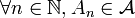
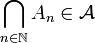
  si alors .

• Si est une famille de tribus sur X, alors est aussi une tribu sur X.

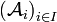
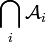
• Le critère suivant est occasionnellement utile pour prouver qu'un ensemble de parties est une tribu :

On le prouve facilement en remarquant que pour toute suite d'éléments de (a priori non disjoints) on peut écrire :

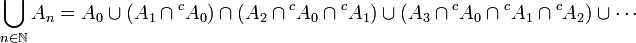
D'autres sources fournissent une variante de cette proposition, en posant comme troisième condition la stabilité par réunion dénombrable croissante. Si on est familier du vocabulaire défini à l'article « lemme de classe monotone », cet énoncé peut se dire ainsi : tout λ-système qui est aussi un π-système est une σ-algèbre.