Valeur d'adhérence - Définition

Introduction

En topologie, si est une suite à valeurs dans un ensemble E, une valeur d'adhérence de la suite (u_n) est un point de E près duquel s'accumulent une infinité de termes de la suite. Pour donner un sens mathématique à cela, il faut pouvoir mesurer la proximité, ce qui nécessite de munir E d'une topologie. La notion de valeur d'adhérence dépend alors de la topologie choisie. Dans un espace où tout point admet une base dénombrable de voisinages (c'est le cas notamment dans un espace métrique, comme ou ) les valeurs d'adhérence d'une suite sont les limites de ses sous-suites. Cette dernière propriété est souvent prise comme définition d'une valeur d'adhérence, mais n'est cependant pas équivalente à la définition la plus générale.

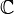
Cas des suites réelles

Le fait que soit un espace métrique permet de donner plusieurs caractérisations équivalentes de l'ensemble des valeurs d'adhérence d'une suite réelle.

Définition et caractérisation

Soient une suite réelle et a un nombre réel, on dit que a est une valeur d'adhérence de (u_n) s'il existe une sous-suite de (u_n) qui converge vers a.

Ceci est équivalent aux deux propriétés suivantes :

1. 
2. l'ensemble est infini.

La deuxième propriété n'est qu'une reformulation ensembliste de la première. Pour montrer l'équivalence de la première propriété avec la définition, il suffit de remarquer que le ε peut être aussi petit que l'on veut, ce qui permet de trouver une sous-suite qui converge vers a. Plus précisément, on a la démonstration suivante :

Exemples

• la suite (( − 1)ⁿ) admet 1 et − 1 comme valeurs d'adhérence. En effet, les termes pairs sont constants à 1 et les termes impairs constants à − 1.

• la suite (sin(n)) admet l'intervalle [ − 1,1] comme ensemble de valeurs d'adhérence. Ceci résulte du fait que est dense dans .

• la suite (( − 1)ⁿn) n'admet pas de valeur d'adhérence dans . Mais dans la droite réelle achevée, la même suite admet et comme valeurs d'adhérence.

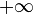
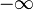
• la suite (( − 1)ⁿn + n) admet 0 comme unique valeur d'adhérence mais ne converge pas. Dans la droite réelle achevée, la même suite admet et 0 comme valeurs d'adhérence.

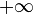
Ensemble des valeurs d'adhérence

Les exemples montrent que l'ensemble des valeurs d'adhérence d'une suite peut être vide ou avoir un ou plusieurs éléments, voire une infinité.

Cet ensemble F est toujours fermé. En effet, la formulation ensembliste de la définition est :

Ce qui montre que F est fermé, comme intersection de fermés.

Dans le cas d'une suite réelle, le plus petit et le plus grand élément de ce fermé sont respectivement les limites inférieure et supérieure de la suite.