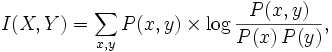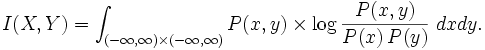Information mutuelle - Définition
Introduction
Dans la théorie des probabilités et la théorie de l'information, l'information mutuelle de deux variables aléatoires est une quantité mesurant la dépendance statistique de ces variables. Elle se mesure souvent en bit.
L'information mutuelle d'un couple (X,Y) de variables représente leur degré de dépendance au sens probabiliste. Ce concept de dépendance logique ne doit pas être confondu avec celui de causalité physique, bien qu'en pratique l'un implique souvent l'autre.
Informellement, on dit que deux variables sont indépendantes si la réalisation de l'une n'apporte aucune information sur la réalisation de l'autre. La corrélation est un cas particulier de dépendance dans lequel la relation entre les deux variables est strictement monotone.
L'information mutuelle est nulle ssi les variables sont indépendantes, et croit lorsque la dépendance augmente.
Définition
Soit (X,Y) un couple de variables aléatoires de densité de probabilité jointe données par P(x,y). Notons les distributions marginales P(x) et P(y). Alors l'information mutuelle est dans le cas discret:
et, dans le cas continu:
Propriétés
- I(X, Y) = 0 ssi X et Y sont des variables aléatoires indépendantes.
- L'information mutuelle est positive ou nulle.
- L'information mutuelle est symétrique.
- 'Data processing theorem': si g1 et g2 sont deux fonctions mesurables alors
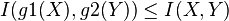
Plusieurs généralisations de cette quantité à un nombre plus grand de variables ont été proposées, mais aucun consensus n'a encore émergé.