Calculs de longueur - Définition

Le but de cet article est de rassembler des 'techniques mathématiques' visant à faciliter le calcul des longueurs, que ce soit dans un plan ou dans un repère. Les formules et astuces utilisées se trouvent dans les articles Aire de surfaces usuelles et Volume de solides usuels.

Calculs sur les triangles

• Configuration 1 : Vous savez l'aire du triangle et sa base, on vous demande de déterminer sa hauteur. Il suffit d'utiliser la formule de l'aire d'un triangle sous forme d'équation en prenant la hauteur comme l'inconnue :

= A

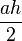
Alors ah = 2A (produit en croix)

Donc h =

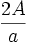
où A est l'aire du triangle

• Configuration 2 : Vous avez les longueurs des 2 côtés d'un triangle, on vous demande de déterminer la longueur du 3^e côté

Dans le cas d'un triangle rectangle :

Il vous suffit d'utiliser le célèbre théorème de Pythagore qui s'énonce comme suit :

" Le carré de l'hypoténuse est égal à la somme des carrés des 2 autres côtés "

Mathématiquement, cela donne :

c² = a² + b²

donc c =

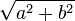
Si vous connaissez l'hypoténuse et un des 2 autres côté, a ou b, l'équation devient :

a =

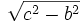
ou

b =

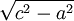
Rappel : L'hypoténuse est le côté opposé à l'angle droit. C'est le côté le plus long.

• Configuration 3 : Connaissant les 2 côtés a et b d'un triangle ainsi qu'une de ses médianes notée m, on vous demande de déterminer la longueur de la base du triangle notée c:

Pour ce faire, on utilise la formule du théorème dit des médianes :

a² + b² = 2m² + c²

Dans notre exemple, on en déduit que :

c² =

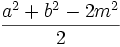
donc

c =

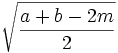
c étant la base du triangle