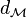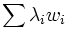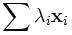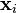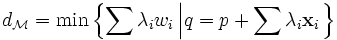Distance de chanfrein - Définition

Les distances de chanfrein sont des distances discrètes utilisant des masques dont les poids sont des entiers. Les distances de chanfrein sont rapides à calculer sur une machine. Bien qu'elles soient plus précises que les distances discrètes d4 et d8, elles ne fournissent qu'une approximation de la distance euclidienne.

Définition

Une pondération est un couple où est un point et w un entier. Un masque est un ensemble fini de pondérations : . Un masque de chanfrein est un masque possédant une symétrie centrale, dont les poids sont strictement positifs et les déplacements non nuls.

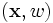
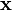
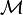
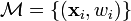
Il est possible de trouver un chemin entre deux points p et q en utilisant les déplacements d'un masque de chanfrein. Soit un masque de chanfrein, alors

,

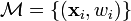
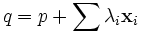
où λ_i est un entier qui correspond au nombre de fois que le déplacement .

Distance de chanfrein

Une distance de chanfrein entre deux points p et q d'un espace discret est le coût minimal de tous les chemins de longueur finie entre p et q et utilisant les déplacements du masque  :

.