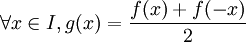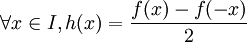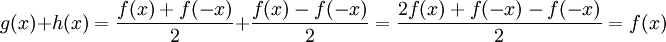Fonctions paires et impaires - Définition
Une fonction
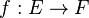
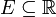
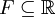
- paire si et seulement si pour tout
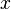

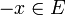
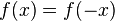
- impaire si et seulement si pour tout
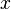

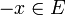
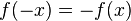
Les appellations "paire" et "impaire" proviennent du fait que toutes les fonctions
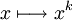
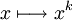
Utilisation
La parité des fonctions sert par exemple à n'étudier la fonction que sur la moitié de son intervalle de définition, l'autre moitié étant déduite par symétrie. On remarquera qu'une fonction impaire définie en 0 est nulle en ce point.
Décomposition en fonctions paires et impaires
Si E est un sous-ensemble de

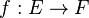
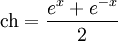
Soit I un sous-ensemble de

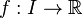
Existence
- Soient g et h deux fonctions de I dans

-
- On sait alors que g est paire car
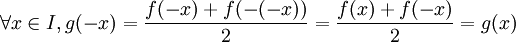
- et également que h est impaire car
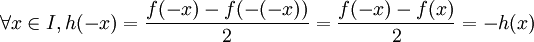
-
- On a donc f = g + h.
Unicité
- Supposons que f = k + l, où
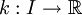
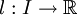
-
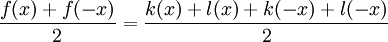
-
- On a donc que k(x) = g(x) et de même, l(x) = h(x). La décomposition de f = g + h est donc unique.
Représentation graphique
Soit f une fonction définie sur E et (Cf) sa représentation graphique dans un repère orthogonal
- f est une fonction paire si et seulement si (Cf) est symétrique par rapport à l'axe (Oy)
- f est une fonction impaire si et seulement si (Cf) est symétrique par rapport au point O
Mais, une fonction dont la courbe représentative possède un axe ou un centre de symétrie n'est pas forcément paire ou impaire : il est nécessaire que le centre soit O ou l'axe soit (Oy).
Quelques propriétés
- La seule fonction qui est à la fois paire et impaire est la fonction nulle (fonction constante égale à 0).
- En général, la somme d'une fonction paire et une fonction impaire n'est ni paire ni impaire ; ex : x + x2.
- La somme de deux fonctions paires donne une fonction paire, et toute constante multiple d'une fonction paire est paire.
- La somme de deux fonctions impaires donne une fonction impaire, et toute constante multiple d'une fonction impaire est impaire.
- Le produit de deux fonctions paires donne une fonction paire.
- Le produit de deux fonctions impaires donne aussi une fonction paire.
- Le produit d'une fonction paire et une fonction impaire donne une fonction impaire.
- Le quotient de deux fonctions paires donne une fonction paire.
- Le quotient de deux fonctions impaires donne une fonction impaire.
- Le quotient d'une fonction paire et une fonction impaire donne une fonction impaire.
- La dérivée d'une fonction paire est une fonction impaire.
- La dérivée d'une fonction impaire est une fonction paire.
- Une primitive d'une fonction impaire n'est pas forcément paire mais si E est un intervalle, toute primitive d'une fonction impaire sur E est une fonction paire.
- Une primitive d'une fonction paire n'est pas forcément impaire mais si E est un intervalle, la primitive d'une fonction paire sur E qui s'annule en 0 est une fonction impaire.
- La composée de deux fonctions impaires donne une fonction impaire.
- La composée f o g d'une fonction quelconque f avec une fonction paire g donne une fonction paire.
- La composée g o f d'une fonction paire g avec une fonction impaire f donne une fonction paire.