Double produit de quaternions - Définition
Il est possible de calculer un double produit de quaternions, c'est-à-dire une expression de la forme :
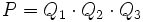
dans laquelle il n'est pas nécessaire d'écrire des parenthèses puisque le produit est associatif.
Intéressons-nous au cas particulier dans lequel les quaternions extrêmes
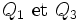
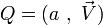
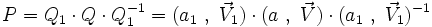
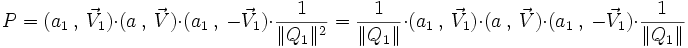
.
Comme les quaternions
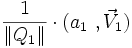
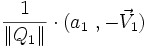
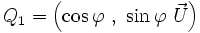
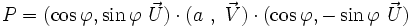
En tenant compte de la distributivité du produit, on peut écrire :
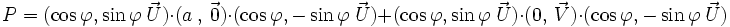
Ainsi le quaternion
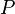
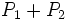
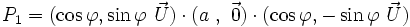
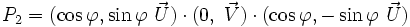
Comme
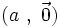
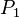
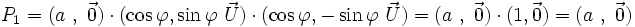
Par conséquent, on a :
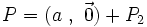
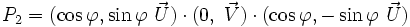
Portons donc notre attention sur le quaternion
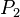
![P_2 = \left[-\sin \varphi\ (\vec U\cdot \vec V), \cos \varphi\ \vec V+\sin \varphi\ (\vec U\wedge\vec V)\right]\cdot \left[\cos \varphi, -\sin \varphi\ \vec U\right]](https://static.techno-science.net/illustration/Definitions/autres/3/3f7cb1035f78620c9eafe2f6f324e8d2_e9bf95a74b382bf7f0cb74b9011fa9dc.png)
![\begin{matrix}P_2 = \big[ &-&\sin \varphi\ \cos \varphi\ (\vec U\cdot \vec V) &+& \sin \varphi\ \cos \varphi\ (\vec V\cdot \vec U) &+& \sin^2 \varphi\ (\vec U\wedge\vec V)\cdot \vec U,&\ \\\ &+& \sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U &+& \cos^2\varphi\ \vec V &+& \sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V)&\ \\&-& \sin \varphi\ \cos \varphi\ (\vec V\wedge\vec U) &-& \sin^2\varphi\ (\vec U\wedge \vec V)\wedge \vec U&\ &\ &\big] \end{matrix}](https://static.techno-science.net/illustration/Definitions/autres/b/b7f1d76f1af2d98446e61654dbe6c5d9_3546e813065dac3353426af93b991bf5.png)
En éliminant le produit mixte
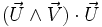
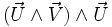
![P_2 = \Bigg[0 \ ,\ \sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U +\ \cos^2\varphi\ \vec V + 2\sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) - sin^2\varphi\ \left[(\vec U\cdot \vec U)\ \vec V - (\vec V\cdot \vec U)\ \vec U \right]\Bigg]](https://static.techno-science.net/illustration/Definitions/autres/c/c9fb60a405d1083c756cd9ea979f1fda_2d7c177e3d4321aff81534ae47b3adee.png)
puis successivement :
![P_2 = \Bigg[0 \ ,\ 2\sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U + \left[\cos^2\varphi\ - \sin^2\varphi\ (\vec U\cdot \vec U)\right]\,\vec V\ +\ 2\sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) \Bigg]](https://static.techno-science.net/illustration/Definitions/autres/a/a51f4068030bf2996b25c494126be9b6_cd74ad9d90981695f5a3124f97c322a6.png)
![P_2 = \Bigg[0 \ ,\ 2\sin^2\varphi\ (\vec U\cdot \vec V)\ \vec U + \left[\cos^2\varphi\ - \sin^2\varphi\right]\vec V\ +\ 2\ \sin \varphi\ \cos \varphi\ (\vec U\wedge\vec V) \Bigg]](https://static.techno-science.net/illustration/Definitions/autres/3/3813f1ae98b62e5234e77e9131df5788_08fe98eda76bba69bc721d5f936483e8.png)
![P_2 = \left[0 \ ,\ \cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V) \right]](https://static.techno-science.net/illustration/Definitions/autres/0/0feefeb8cdb47d4baf27d3db8a279e11_da2dce94490b9ce05d08ae4cd974d874.png)
Ainsi, il est établi que si le vecteur
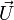
![(\cos \varphi, \sin \varphi \ \vec U)\cdot (a\ ,\ \vec V)\cdot (\cos \varphi, -\sin \varphi \ \vec U) = (a\ ,\ \vec 0) + \left[0 \ ,\ \cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V) \right]](https://static.techno-science.net/illustration/Definitions/autres/7/7832e13022fd5d43d7f604778466a4ed_55b333b019ba3f223b388241dc0dfee4.png)
Or, dans l'expression qui apparaît dans la composante vectorielle du deuxième quaternion du membre de droite de cette égalité, à savoir :
![\cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V)]](https://static.techno-science.net/illustration/Definitions/autres/d/d430fabc9b7eed0351675865c097b89c_b6a96da695665b2c5027121695792a73.png)
on peut reconnaître l'expression vectorielle du vecteur transformé du vecteur
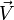
![\mathbf R\left[2\,\varphi\,\,; \vec U\right]](https://static.techno-science.net/illustration/Definitions/autres/7/7fbb38e15013d3d30e9c54df429d3d5a_8f8d9d869196f39366af3cf93d2295a3.png)
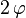
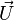
De la démonstration précédente, on peut tirer l'importante conclusion générale suivante :
Conclusion
Dans la rotation
![\mathbf R\left[2\,\varphi\,\,; \vec U\right]](https://static.techno-science.net/illustration/Definitions/autres/7/7fbb38e15013d3d30e9c54df429d3d5a_8f8d9d869196f39366af3cf93d2295a3.png)
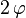
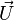
le transformé
![\vec V' = \mathbf R_{\left[2\varphi, \vec U\right]}(\vec V)\,](https://static.techno-science.net/illustration/Definitions/autres/4/4ff355d36ac46fcc03852c720b405e0c_c0319d9afdcfc2683ad0de0acd86617c.png)
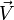
- soit grâce à l'égalité quaternionique suivante :
|
|
- soit grâce à l'égalité vectorielle :
|
|
| Articles de mathématiques en rapport avec la notion de nombre | |
| Définition des nombres · Entiers naturels · Entiers relatifs · Nombres transfinis · Nombres décimaux · Nombres rationnels · Nombres constructibles · Nombres algébriques · Nombres transcendants · Nombres calculables · Nombres réels · Nombres complexes · Nombres hypercomplexes · Quaternions · Octonions · Sédénions · Nombres hyperréels · Nombres surréels · Nombres ordinaux · Nombres cardinaux · Nombres p-adiques · Nombres normaux · Suite d'entiers · Constantes mathématiques · Grands nombres · Nombres incalculables · Infiniments petits · Infini | |
![\left(0 \ ,\ \mathbf R_{\left[2\varphi, \vec U\right]}(\vec V)\right) = (\cos \varphi, \sin \varphi \ \vec U)\cdot (0,\ \vec V)\cdot (\cos \varphi, -\sin \varphi \ \vec U)\ \ \ \,](https://static.techno-science.net/illustration/Definitions/autres/e/ef0b1e8d06cd87c686ace332438342f9_68cbc3ac858be4388302c109516f6bd2.png)
![\mathbf R_{\left[2\varphi, \vec U\right]}(\vec V) = \cos 2\,\varphi\ \, \vec V\ + \ (1-\cos 2\,\varphi)\,(\vec U\cdot \vec V)\ \vec U + \ \sin 2\,\varphi\ (\vec U\wedge\vec V)]\ \ \ \,](https://static.techno-science.net/illustration/Definitions/autres/3/3e34f5e39217da6d3d077a5fb18fb4e0_a73132cdaa69746717d69ae43bdca0a5.png)

















































