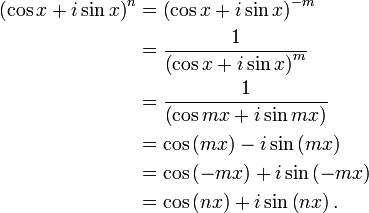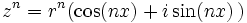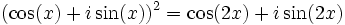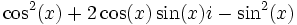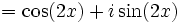Formule de De Moivre - Définition
La formule de De Moivre (en référence à Abraham de Moivre) ou formule de Moivre (voir l'article Particule (onomastique) pour une explication sur le " de ") dit que pour tout nombre réel x et pour tout nombre entier n :
-
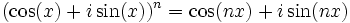
ou encore
-
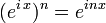
Cette formule est importante car elle met en relation les nombres complexes (i étant l'unité imaginaire) et la trigonométrie.
L'expression " cos(x) + i·sin(x) " est parfois abrégée en " cis x ".
Démonstration de la formule
Considérons trois cas.
Pour n > 0, nous procédons par récurrence. Lorsque n = 1, la formule est vraie. Soit k un entier naturel supérieur à 1 tel que la formule soit vraie. Cela signifie que
Nous avons
Nous en déduisons que la formule est vraie au rang k + 1.
D'après le principe de récurrence, il s'ensuit que la formule est vraie pour tous les entiers naturels non nuls.
Lorsque n = 0, la formule est vraie puisque cos(0x) + isin(0x) = 1 + i0 = 1, et par convention z0 = 1.
Lorsque n < 0, nous considérons un entier naturel strictement positif m tel que n = − m. Ainsi
Ainsi le théorème est vrai pour tous les entiers relatifs n c.q.f.d..
Utilisations de la formule de De Moivre
Cette formule est utilisée pour rechercher les puissances n-ièmes et les racines n-ièmes de nombres complexes sous forme trigonométrique :
ainsi que pour obtenir les formes de cos(nx) et sin(nx) en fonction de sin(x) et cos(x).
Par exemple, pour avoir cos(2x) et sin(2x), on égale :
On a
On égalise les parties réelles et imaginaires :
-
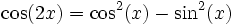
-
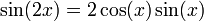
On obtient les formules trigonométriques de duplication.
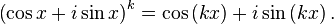
![\begin{alignat}{2} \left(\cos x+i\sin x\right)^{k+1} & = \left(\cos x+i\sin x\right)^{k} \left(\cos x+i\sin x\right)\\ & = \left[\cos\left(kx\right) + i\sin\left(kx\right)\right] \left(\cos x+i\sin x\right) \qquad {\rm dapr\grave es\; l^{\prime} hypoth \grave ese\; de\; r\acute ecurrence}\\ & = \cos \left(kx\right) \cos x - \sin \left(kx\right) \sin x + i \left[\cos \left(kx\right) \sin x + \sin \left(kx\right) \cos x\right]\\ & = \cos \left[ \left(k+1\right) x \right] + i\sin \left\{ \left(k+1\right) x \right\} \qquad {\rm d^{\prime}apr\grave es\; les\; formules\; trigonom\acute etriques} \end{alignat}](https://static.techno-science.net/illustration/Definitions/autres/2/2c940ce3b7fa5a8df047b985456fd63a_03ea415fcc3273e86e1bd24f144b4200.png)