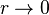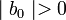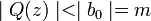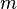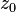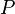Théorème de d'Alembert-Gauss - Définition
Le théorème de d'Alembert-Gauss, simplement appelé théorème de d'Alembert ou encore théorème fondamental de l'algèbre, s'énonce de la façon suivante :
- " Tout polynôme de degré supérieur ou égal à 1 à coefficients dans le corps


En d'autres termes, le corps

Ce théorème fut énoncé pour la première fois par Albert Girard. Jean le Rond d'Alembert en donna une démonstration presque complète, dans son Traité de dynamique. Carl Friedrich Gauss en donna la première démonstration rigoureuse au début du XIXe siècle.
La dénomination " théorème fondamental de l'algèbre " fait sourire certains car il s'agit d'un théorème " exogène " à l'algèbre, au sens où l'on n'en connaît pas de démonstration qui évite de faire appel à des outils d'analyse.
Une preuve très concise repose sur le théorème de Liouville en analyse complexe. À cet effet, on considère un polynôme P à coefficients complexes, de degré au moins égal à 1. On suppose qu'il n'a aucune racine : dès lors, la fonction rationnelle 1 / P est entière et bornée (car elle tend vers 0 à l'infini) ; du théorème de Liouville, on déduit qu'elle est constante, ce qui contredit l'hypothèse sur le degré, et prouve ainsi par l'absurde l'existence d'au moins une racine de P.
Autre démonstration
Soit
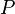
Notons:
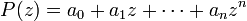
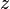

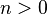
D'après l'inégalité triangulaire, on a:
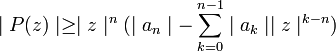
On en déduit que:
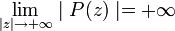
Notons
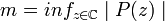
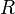
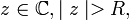
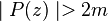
On en déduit que
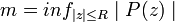
Le disque
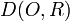
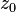
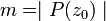
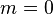
Supposons que ce n'est pas le cas.
Notons
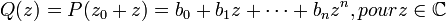
Soit
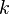
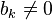
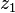
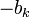
Notons:
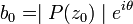
Alors pour
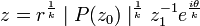
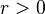
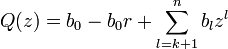
D'après l'inégalité triangulaire, on a:
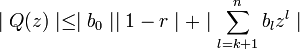
Donc pour
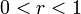
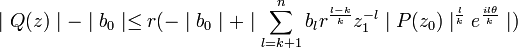
Or quand