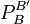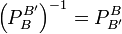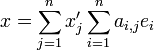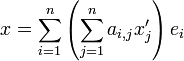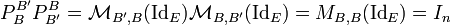Matrice de passage - Définition
Une matrice de passage permet d'écrire des formules de changement de base pour les représentations matricielles des vecteurs, des endomorphismes, des formes bilinéaires.
Définition
Soient
Soient deux bases
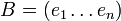
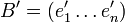
On définit ainsi la matrice de passage de B à B', notée
-
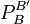
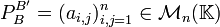
![\forall j \in [\![1,n]\!], \quad e'_j=\sum_{i=1}^n a_{i,j}e_i](https://static.techno-science.net/illustration/Definitions/autres/2/27d81ad5b0f39251d7f260f525f7cb28_003c8c6078324e9b3157eeb0bd05bbf3.png)
![\forall j \in [\![1,n]\!], \quad e'_j=\sum_{i=1}^n a_{i,j}e_i](https://static.techno-science.net/illustrationWebp/Definitions/autres/2/27d81ad5b0f39251d7f260f525f7cb28_003c8c6078324e9b3157eeb0bd05bbf3.png)
Les colonnes de cette matrice sont les matrices représentatives des vecteurs de la nouvelle base, exprimés dans l'ancienne base.
On peut aussi interpréter la matrice de passage comme la matrice représentative de l'application identité, de E muni de la base B' dans E muni de la base B. On a
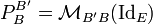
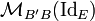
Théorème
Enoncé
Soit un vecteur
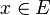
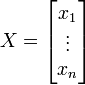
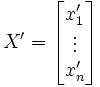
Alors
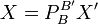
Démonstration
La décomposition du vecteur dans les deux bases nous donne
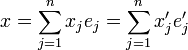
De plus,
![\forall j \in [\![1,n]\!], e'_j=\sum_{i=1}^n a_{i,j}e_i](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4985b15a157beedf4bb7e5bc1ae62b70_6d0bd72d0c50b593d3d1bc82706f79ef.png)
Par substitution,
La décomposition du vecteur étant unique dans chaque base, on peut procéder à l'identification des coefficients:
-
![\forall i \in [\![1,n]\!], x_i=\sum_{j=1}^n a_{i,j} x'_j = \left(P_B^{B'}\cdot X'\right)_i](https://static.techno-science.net/illustration/Definitions/autres/c/c758f44c1873c9f52be5143d291768ed_265c9b68b0c8176fe6d00fcbebc60b07.png)
![\forall i \in [\![1,n]\!], x_i=\sum_{j=1}^n a_{i,j} x'_j = \left(P_B^{B'}\cdot X'\right)_i](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c758f44c1873c9f52be5143d291768ed_265c9b68b0c8176fe6d00fcbebc60b07.png)
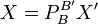
Inversibilité
Soient B et B' deux bases de E Alors
