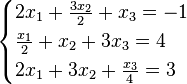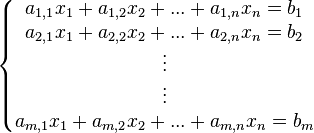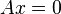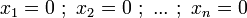Système d'équations linéaires - Définition
En mathématiques et particulièrement en algèbre linéaire, un système d'équations linéaires est un ensemble d'équations linéaires. Par exemple :
Le problème est de trouver les valeurs des inconnues
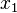
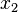
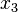
Le résolution des systèmes d'équations linéaires appartient aux problèmes les plus anciens dans les mathématiques et ceux-ci apparaissent dans beaucoup de domaines, comme dans le traitement des signaux numériques ou dans l'approximation de problèmes non-linéaires en analyse numérique. Un moyen efficace de résoudre un système d'équations linéaires est donné par l'élimination de Gauss-Jordan ou par la décomposition de Cholesky ou encore par la décomposition LU. Dans les cas simples, la règle de Cramer peut également être appliquée.
En général, un système de m équations linéaires à n inconnues peut être écrit sous la forme suivante :
Où x1,...,xn sont les inconnues et les nombres ai,j sont les coefficients du système.
Un système d'équations linéaires peut aussi s'écrire sous la forme matricielle :
- Ax = b
avec :
-

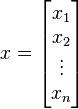
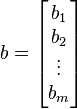
L'élimination de Gauss-Jordan, mentionnée ci-dessus, s'applique à tous ces systèmes, même si les coefficients viennent d'un corps arbitraire. Si le corps est infini (comme c'est le cas pour les nombres réels et pour les nombres complexes) alors seulement les trois cas suivants sont possibles pour n'importe quel système donné d'équations linéaires:
- Le système n'a pas de solution.
- Le système a un unique n-uplet solution.
- Le système a une infinité de n-uplets solutions.
Un système de la forme :
est appelé système d'équations linéaires homogènes. Tout les systèmes homogènes admettent au moins une solution :
Cette solution est la solution nulle ou triviale. Les systèmes homogènes admettent une infinité de solutions si le système contient moins d'équations que d'inconnues.