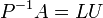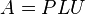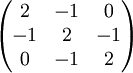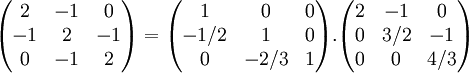Décomposition LU - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Applications - Exemple - Calcul de la décomposition - Existence, unicité

Introduction

En algèbre linéaire, la décomposition LU est une méthode de décomposition d'une matrice comme produit d'une matrice triangulaire inférieure L (comme "Low", bas) et une matrice triangulaire supérieure U (comme "Up", haut). Cette décomposition est utilisée en analyse numérique pour résoudre des systèmes d'équations linéaires.

Définition

Soit A une matrice inversible. La matrice A peut être décomposée ainsi :

où P est une matrice de permutation (de même pour P^-1), L est une matrice triangulaire inférieure avec des 1 sur la diagonale et U une matrice triangulaire supérieure. Parfois, la matrice de passage P peut être choisie afin d'être une matrice identité. Dans ce cas, la décomposition devient $A = L U .$

Applications

Résoudre un système d'équations linéaires

Cette factorisation matricielle permet de résoudre des systèmes d'équations linéaires où les coefficients des inconnues sont les mêmes, mais avec plusieurs seconds membres différents. Soit à déterminer le vecteur d'inconnues {x} associé au second membre {b} :

A {x} = {b}

Ce problème est donc équivalent à la résolution de

L U {x} = {b}

ou encore

L {U x} = {b}

que l'on peut mettre, en posant

{U x} = {y}

sous la forme :

L {y} = {b}

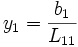
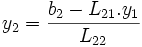
On trouve les composantes de y par des substitutions élémentaires, puisque d'abord $y_1 = \frac{b_1}{L_{11}}$ , puis $y_2 = \frac{b_2-L_{21}.y_1}{L_{22}}$ , etc.

Cette étape est appelée descente, puisqu'on résout le système en descendant de $y 1$ à $y n$ . Il reste à calculer les composantes du vecteur {x} en résolvant le système triangulaire supérieur :

U {x} = {y}

ce qui se fait de manière similaire, mais en calculant d'abord $x n$

, etc. en remontant (étape dite de remontée).

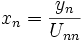
Remarque. - Les matrices triangulaires L et U auraient pu être inversées aisément en utilisant l'élimination de Gauss-Jordan. Mais si l'on compte simplement le nombre d'opérations que cela représente pour un système à n équations, on trouvera que la complexité algorithmique du calcul des matrices inverses est supérieure, de sorte que si l'on veut résoudre ce système pour divers b, il est plus intéressant de réaliser la décomposition LU une fois pour toute et d'effectuer les substitutions de descente-remontée pour les différents b plutôt que d'utiliser l'élimination de Gauss-Jordan à de multiples reprises. Ainsi, dans la plupart des publications d'analyse numérique, lorsque la matrice A a été factorisée sous forme LU ou Cholesky (cf. infra, § Le cas symétrique ), on écrit par abus $b = A - 1 x$ pour signifier que le calcul de b peut se faire par cette méthode de descente-remontée. Il est sous-entendu qu'il n'est absolument pas question d'utiliser l'algorithme en calculant la matrice inverse $A - 1$ de A, ce qui serait inutilement coûteux en temps de calcul.

Inverser une matrice

Les matrices L et U peuvent être utilisées pour déterminer l'inverse d'une matrice. Les programmes informatiques qui implémentent ce type de calcul, utilisent généralement cette méthode.

Calcul d'un déterminant

Si A est sous forme LU ou PLU, son déterminant se calcule facilement : $det(A) = det(P)det(L)det(U)$ . Les trois déterminants de ce produit sont très simples à calculer (matrices triangulaires ou de permutations).