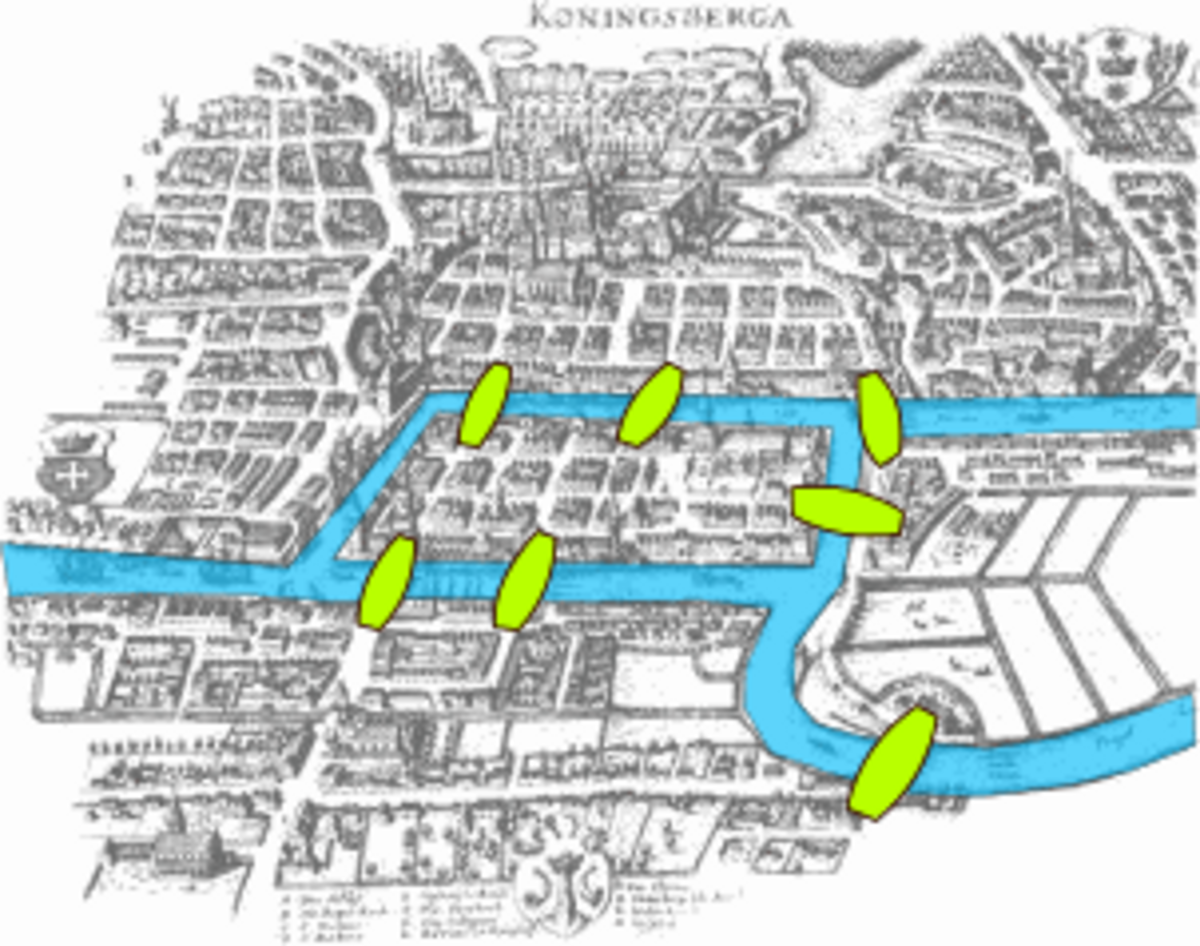
Problème des sept ponts de Königsberg - Définition

Le problème des sept ponts de Königsberg est un problème mathématique historique, qui fit la célébrité de la ville de Königsberg (aujourd'hui Kaliningrad). Sa résolution fut recherchée par ses habitants tout au long du XVIII^e siècle.

Le problème est le suivant :

Étant donné que la ville est construite sur deux îles reliées au continent par six ponts, et entre elles par un pont, trouver un chemin quelconque permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ, étant entendu qu'on ne peut traverser l'eau qu'en passant par les ponts.

Résolution du problème

Le problème était insoluble, et c'est Leonhard Euler qui, le premier, donna à ce problème la première résolution mathématique formelle en le ramenant à un problème de la théorie des graphes. Sa démarche peut être schématisée de cette manière :

→ →

Le problème se ramène alors à la recherche d’un cycle eulérien (chaîne passant par toutes les arêtes du graphe une et une seule fois, et revenant à son point de départ), ce qui n’est possible que si le graphe associé au problème ne possède aucun sommet de degré impair. Celui de la ville de Königsberg en possède 4 (chaque berge est le départ de 3 ou 5 ponts), le problème n'admet donc pas de solution.

Si le problème avait consisté à n'emprunter les ponts qu'une seule fois sans pour autant revenir à son point de départ, cela reviendrait à la recherche d'une chaîne eulérienne (chaîne passant par toutes les arêtes du graphe une et une seule fois), ce qui n'est possible que si le graphe associé au problème possède 0 ou 2 sommets de degré impair. Dans le deuxième cas, le chemin doit partir d'un des sommets de degré impair, et aboutir à l'autre sommet de degré impair.