Hypocycloïde - Définition
Une hypocycloïde est une courbe plane transcendante, trajectoire d'un point fixé à un cercle qui roule sans glisser sur un autre cercle dit directeur et à l'intérieur de celui-ci. Il s'agit donc d'un cas particulier de cycloïde à centre, qui est une catégorie de courbe cycloïdale.
Étymologie et histoire
Le mot est une extension de cycloïde, inventé en 1599 par Galilée, et a la même étymologie : il vient du grec hupo (sous), kuklos (cercle, roue) et eidos (forme, " semblable à ").
La courbe elle-même fut étudiée par Albrecht Durer en 1525, Rømer en 1674 (qui la baptisa) et Daniel Bernoulli en 1725.
Définition mathématique
Une hypocycloïde peut être définie par l'équation paramétrique suivante :
où
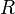

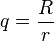
Propriétés
La courbe est formée d'arcs isométriques (appelés arches) séparés par des points de rebroussements. Si q est rationnel (et peut donc s'écrire q=a/b où a et b sont des entiers), a représente le nombre d'arches de la courbe. On peut aussi voir ces deux grandeurs de la manière suivante :
- a représente le nombre de rotations du cercle roulant nécessaires pour ramener le point mobile à sa position de départ,
- b représente le nombre de tours du cercle de base nécessaires au cercle roulant pour revenir au point de départ.
Les points de rebroussements sont obtenus pour
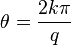
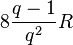
Si q est entier, la longueur totale de la courbe vaut
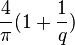
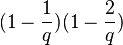
Le théorème de la double génération prouve qu'une hypocycloïde est aussi une péricycloïde, c'est-à-dire la courbe décrite par un point d'un cercle de rayon r+R roulant sans glisser sur ce cercle directeur en le contenant.
Les petites oscillations du pendule de Foucault forment également une hypocycloïde.
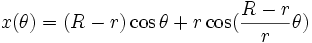
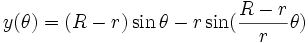
![x(\theta) = r \left[(q-1) \cos \theta + \cos (q-1) \theta \right] \,](https://static.techno-science.net/illustration/Definitions/autres/d/d652b66bc44d5eb0e25c98e8fee4ec94_ba0295ed1a3ba85b75c7e2386ff6abf6.png)
![y(\theta) = r \left[(q-1) \sin \theta - \sin (q-1) \theta \right]\,](https://static.techno-science.net/illustration/Definitions/autres/2/256276750acbebca346d29e06c196d7d_05fc6ecc632de98e4d5f7e0b74358ef1.png)

















































