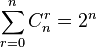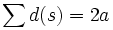Preuve bijective - Définition
En mathématique, la preuve bijective est une technique de démonstration qui consiste à considérer une application bijective entre deux ensembles et à dénombrer chacun de ces ensembles, pour montrer que les expressions obtenues, correspondant à un même cardinal, sont égales. Dans le cas particulier où l'application bijective est l'identité d'un ensemble, cela revient à compter le nombre d'éléments de l'ensemble de deux façons différentes, pour établir une égalité entre les nombres résultants. Nous pourrions appeler cette dernière méthode, le double comptage. Autrement dit, nous pouvons considérer deux ensembles X et Y et les dénombrer tous les deux, puis au moyen d'un bijection f de X sur Y, en déduire que les résultats sont identiques; ou nous pouvons également considérer un ensemble fini X et le dénombrer par une méthode A, puis une méthode B.
En identifiant les éléments des deux ensembles équipotents, on peut toujours se ramener à un dénombrement d'un même ensemble de différentes façons.
Exemples
Par exemple, considérez le nombre de manières desquelles un comité peut être formé à partir d'un total de n personnes.
Première méthode : il y a deux possibilités pour chaque personne. À chaque fois une personne peut faire partie du comité ou ne pas en faire partie. Par conséquent il y a un total de
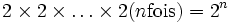
Deuxième méthode : le nombre de membres du comité doit être un nombre entier r compris entre 0 et n. Le nombre de manières desquelles un comité de r personnes peut être formé à partir d'un total de n personnes est
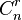
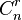
L'égalisation des deux expressions donne
Un exemple de théorème qui est généralement démontré en utilisant une preuve bijective est le théorème qui affirme que tout graphe contient un nombre pair de sommets du degré impair. Soit d(s) le degré du sommet s. Chaque arête du graphe joint exactement deux sommets, ainsi en comptant le nombre d’arêtes joignant chaque sommet, nous avons compté chaque arête exactement deux fois. Par conséquent
où a est le nombre d’arêtes.
La somme des degrés des sommets est donc un nombre pair, ce qui ne pourrait se produire si un nombre impair de sommets avait un degré impair.