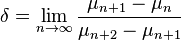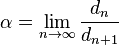Nombres de Feigenbaum - Définition
En mathématiques, les nombres de Feigenbaum ou constantes de Feigenbaum sont deux nombres réels découverts par le mathématicien Mitchell Feigenbaum en 1975. Tous deux expriment des rapports apparaissant dans les diagrammes de bifurcation de la théorie du chaos.
Les diagrammes de bifurcation concernent les valeurs limites prises par les suites de type xn + 1 = μf(xn) où f est une fonction réelle, définie positive et trois fois dérivable sur [0;1] et possédant un maximum unique sur cet intervalle (c’est-à-dire sans maximum relatif) noté xm. Pour une fonction donnée, en dessous d'une certaine valeur de μ, la suite conduit à une limite unique. Au dessus de celle valeur, mais en-dessous d'une autre, la suite finit par osciller entre deux valeurs, puis au-dessus d'une autre valeur, à osciller autour de quatre, etc. Les valeurs de μ séparant deux intervalles sont appelées des bifurcations et sont notée μ1, μ2, etc.
La première constante de Feigenbaum est définie comme la limite du rapport entre deux intervalles successifs de la bifurcation :
Dans le cadre de la fonction logistique où xn + 1 = μxn(1 − xn) (initialement étudiée par Feigenbaum) :
-
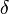
Il apparaît qu'il s'agit également du rapport entre les diamètres de deux cercles successifs sur l'axe de l'ensemble de Mandelbrot.
En conséquence, tout système chaotique qui obéit à cette description bifurquera à la même vitesse. La première constante de Feigenbaum peut être utilisée pour prédire quand le chaos arrivera dans tel système.
La deuxième constante de Feigenbaum est définie comme la limite du rapport entre deux distances successives entre les branches les plus proches de xm (le maximum de la fonction f) :
Toujours dans le cadre de la fonction logistique :
-

Ces constantes s'appliquent à une large classe de systèmes dynamiques. Une hypothèse est que ces deux nombres sont transcendants bien que cela n'ait jamais encore été prouvé.