Modèle d'évaluation des actifs financiers - Définition
Le Modèle d'évaluation des actifs financiers (MEDAF), traduction approximative[1] de l'anglais Capital Asset Pricing Model (CAPM) fournit une estimation de valeur théorique d'un actif financier. Cette théorie prend en compte l'aversion naturelle des investisseurs pour le risque (plus précisément, ils cherchent à maximiser leur profit pour un risque donné, ou à profit donné veulent minimiser le risque pris).
Définition
Le Medaf ou Capital Asset Princing Model explique la réalisation de l'équilibre du marché par l'offre et la demande pour chaque titre. Il permet de déterminer le rendement d'un actif risque par son risque systématique
Les transactions cesseront lorsque les opérateurs auront un portefeuille identique
La formule est une fonction :
- de la mesure du risque systématique de l'actif, c'est-à-dire au risque non diversifiable (l'investisseur diversifiera son portefeuille directement sur le marché), noté
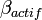
- de la rentabilité espérée sur le marché, notée
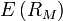
- du taux d'intérêt sans risque (généralement des emprunts d'État), noté
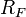
![E(R_{actif}) = R_F + \beta_{actif}\cdot [E(R_M) - R_F]](https://static.techno-science.net/illustration/Definitions/autres/c/cc575bba3d4b39504da4dc545d6440cc_7b2d8b6383fbffe84a7def6c3a8c64be.png)
![[E(R_M) - R_F] \,](https://static.techno-science.net/illustration/Definitions/autres/5/5156408ee615810bf967ce0851831885_e69f67c60ae39f2ce03a5dd1d3f92f0f.png)
Le
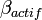
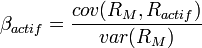
Dans le modèle MEDAF (ou CAPM), on peut montrer que ce coefficient correspond à l'élasticité financière du risque du marché par rapport au risque de l'actif:
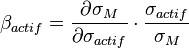
où
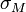
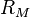

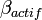
Remise en question
en:Eugene Fama et en:Kenneth French ont publié en 1992 une étude célèbre[2] remettant en cause le CAPM, surnommée depuis le "Beta is dead" paper (" l' article annonçant la mort de Bêta "). Elle attribuait l'essentiel des variations de prix non au bêta mais à deux autres coefficients de marché :
- le Price earning ratio (PER)
- et le ratio capitalisation boursière sur actif net comptable (Price to book value (PBV), appelé aussi, en prenant le ratio inverse, Book to market).
Un modèle devenu populaire en est dérivé, le Three-factor model.
Un modèle allant dans ce sens mais encore plus étendu est l'APT (Arbitrage Pricing Theory) de Ross qui accepte des bêtas multiples dont chacun correspond à un facteur quantifiable particulier.
Enfin, les recherches en Finance comportementale ont introduit d'autres élements, par exemple les sur-réactions et sous-réactions du marché aux informations.

















































