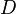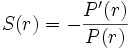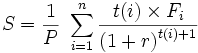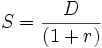Sensibilité (économie) - Définition

En économie, la sensibilité (en anglais : sensitivity) est la variation d'une grandeur économique lorsqu'une autre varie en valeur absolue d'une unité, ou en valeur relative de 1%. Cette notion se rapproche de celle de l'élasticité, celle-ci mesurée systématiquement toutefois par comparaison des valeurs relatives.

Par exemple la sensibilité au prix du pétrole du solde du commerce extérieur d'un pays, ou encore du résultat net d'une entreprise très utilisatrice de cette matière, est la variation de cet indicateur de gestion lorsque ce prix sur le marché au comptant varie de un dollar.

En finance, la sensibilité (en anglais : modified duration) est liée au concept de duration. C'est un indicateur du risque de taux lié à un instrument à taux fixe, comme une obligation.

Définition financière (sensitivité au taux d'intérêt)

Il s'agit de la variation pour 1% de taux (100 points de base) du prix de l'instrument par rapport à son taux actuariel. Comme, pour la plupart des instruments, le prix augmente lorsque les taux diminuent, on considère plutôt le rapport inverse.

Avec :

• le taux actuariel de l'instrument,
• le prix de l'instrument en fonction de son taux actuariel,
• la dérivée du prix de l'instrument par rapport au taux actuariel,

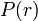
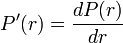
la sensibilité est donc :

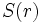
Ordres de grandeur

Schématiquement, une obligation ayant une sensibilité de 5 verra sa valeur baisser d'environ 5% si son taux d'intérêt augmente de 1%, et, inversement, sa valeur augmenter d'environ 5% si les taux baissent de 1%.

Néanmoins, il convient de se souvenir que le prix n'évolue pas de façon linéaire en fonction du taux actuariel et que l'erreur croît avec l'écart de taux qu'on applique.

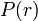
Objectifs et limites

Tout comme la duration, la sensibilité est essentiellerment une mesure patrimoniale, utilisée par les gestionnaires de fonds. Il s'agit en effet du rapport de la mesure première du risque de taux, ,à la valeur actualisée de l'instrument, c'est dire à l'ensemble des capitaux investis, et non à sa valeur nominale.

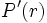
Les professionnels des marchés de taux d'intérêt n'utilisent, eux, comme mesure première du risque de taux actuariel, que seul, non corrigé.

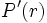
En revanche, la sensibilité moyenne d'un OPCVM à capital variable constitue, pour le public, une mesure importante du risque de taux qu'il présente, puisqu'on souscrit à ce type de placement et qu'on le revend, chaque fois, en montants bruts.

Propriétés

Plus une obligation à taux fixe est longue, plus elle est sensible.

Par ailleurs, comme il s'agit d'une élasticité, la sensibilité possède des propriétés paradoxales. Ainsi, plus le taux nominal d'une obligation à taux fixe est élevé, plus le risque de taux qu'elle présente est élevé. Néanmoins, comme elle est dotée d'un prix élevé en pourcentage du nominal, sa sensibilité sera plus faible que celle d'une obligation de mêmes caractéristiques mais de taux nominal plus faible.

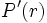
Formules

La sensibilité est donnée par la formule suivante :

avec :

le prix de l'obligation,

le flux (coupon et capital) de la période ,

est l'intervalle de temps, exprimé en années, séparant la date d'actualisation de la date du flux

le taux actuariel de l'obligation.

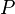
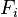
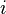
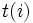
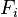
On remarque que la sensibilité peut s'exprimer en fonction de la duration  :