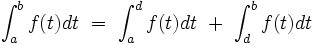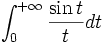Intégrale impropre - Définition
L'intégrale impropre désigne une extension de l'intégrale usuelle, définie par une forme de passage à la limite dans des intégrales. On note en général les intégrales impropres sans les distinguer des véritables intégrales ou intégrales définies, ainsi
est un exemple très classique d'intégrale impropre convergente, mais qui n'est pas définie au sens de l'intégration usuelle (que ce soit l'intégration des fonctions continues par morceaux, l'intégrale de Riemann, ou celle de Lebesgue).
Dans la pratique, on est amené à faire une étude de convergence d'intégrale impropre
- lorsqu'on intègre jusqu'à une borne infinie,
- lorsqu'on intègre jusqu'à une borne en laquelle la fonction n'admet pas de limite finie,
- lorsqu'on englobe un point de non définition dans l'intervalle d'intégration.
Dans chaque cas, on évaluera l'intégrale définie comme une fonction d'une des deux bornes et on prendra la limite de la fonction obtenue lorsque l'argument tend vers la valeur de la borne.
L'intégrale impropre partage un certain nombre de propriétés élémentaires avec l'intégrale définie. Elle ne permet pas d'écrire des résultats d'interversion limite-intégrale.
Intégrale impropre pour les fonctions continues
Définition
Soit
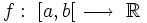
Si la limite
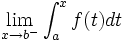
De la même manière, soit
![f :\ ]a, b] \ \longrightarrow \ \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/8/847c3ad35c8cbf3e7f525a8341c0a631_3d7dffd1a8e18eea4884c430f0ea38c6.png)
Si la limite
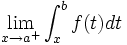
Dans les deux cas on note cette limite
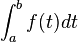
Si la limite existe et est finie on dit que
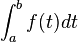
Compatibilité avec l'intégrale définie : si f est en fait continue sur le segment [a,b], on obtient par ces définitions la même valeur que si on calculait l'intégrale définie de f.
Relation de Chasles
Soit
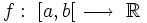
Alors
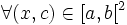
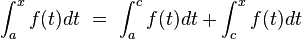
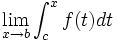
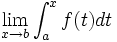
De plus, si
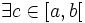
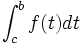
Alors
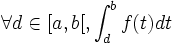
et
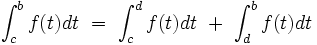
Intégrale impropre bilatère
Soit
![f :\ ]a, b[\ \longrightarrow\ \mathbb{R}](https://static.techno-science.net/illustration/Definitions/autres/8/8b542a1b4bbfd1552685d16271926059_53c3c7b5dc9f9cff2c9189638d1e722f.png)
Soit
![c \in ]a, b[](https://static.techno-science.net/illustration/Definitions/autres/0/0eff8d69467c10b57a87a34915f5b2bd_1bf34e6cdd8d1bfecccf57a49fdda2ed.png)
La relation de Chasles nous dit que
-
- Si
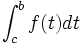
- Alors
![\forall d \in ]a, b[, \int_d^b f(t) dt](https://static.techno-science.net/illustration/Definitions/autres/5/5277052409620d4bb192dfd5b2ba1270_f9f07838abe6f1f9ff431af0ddb7e89c.png)
-
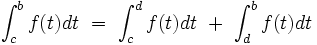
- Si
-
- Si
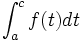
- Alors
![\forall d \in ]a, b[, \int_a^d f(t) dt](https://static.techno-science.net/illustration/Definitions/autres/8/8b1cdec404640e71bca634b67680ad04_a6223b66a749755c767b30611861a8f1.png)
-
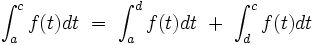
- Si
Quand ces deux conditions sont vérifiées, on appelle intégrale impropre de f sur ]a,b[ la somme