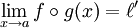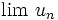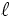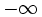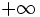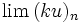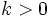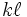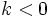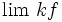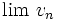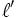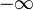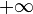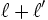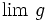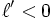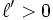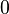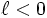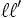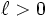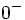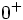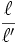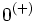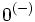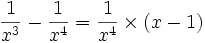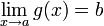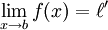Opérations sur les limites - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Cette page est une annexe de l'article limite (mathématiques élémentaires), qui explique comment traduire en termes de limites les opérations usuelles : addition, multiplication, composition...
Tous les résultats listés ici sont valables à la fois pour les limites de fonctions et pour les limites de suites
Opérations algébriques
On considère ici le cas où on effectue les opérations algébriques élémentaires sur des fonctions ou des suites dont on connaît les limites. Dans la plupart des cas on peut conclure mais parfois une étude supplémentaire est nécessaire, on parle de forme indéterminée, ou FI. Ces cas seront traités à part.
Multiplication par un réel
On peut multiplier une suite
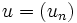
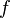
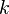
- La suite
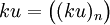
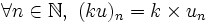
- La fonction
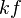
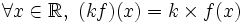
Alors on peut écrire le tableau suivant, selon que la suite converge vers une limite finie
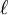
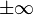
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
On a exactement le même tableau pour les cas d'une fonction
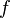
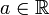
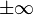
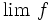
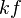
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
Addition
On peut additionner deux suites
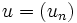
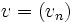
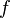
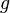
- La suite
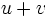
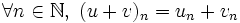
- La fonction
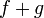
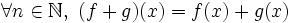
On peut donner la limite de la suite
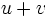
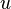
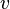
|
|
|||||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
FI | ||
|
|
|
FI |
|
On a exactement le même tableau pour la limite de
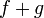
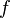
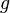
|
|
|||||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
FI | ||
|
|
|
FI |
|
Multiplication
On peut multiplier deux suites
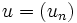
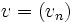
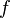
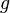
- La suite

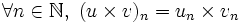
- La fonction
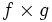
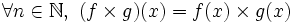
On peut donner la limite de la suite

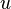
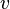
|
|
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
FI | FI | ||
|
|
|
|
FI |
|
|
||
|
|
|
|
FI |
|
|
On a exactement le même tableau pour la limite de
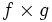
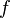
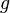
|
|
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
FI | FI | ||
|
|
|
|
FI |
|
|
||
|
|
|
|
FI |
|
|
Division
On peut diviser une suite
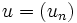
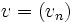
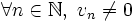
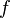
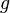
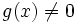
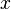
- La suite

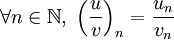
- La fonction
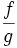
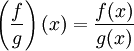
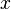
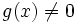
On peut donner la limite de la suite

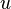
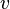
|
|
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
FI | FI |
|
|
||
|
|
|
|
FI | FI |
|
|
||
|
|
|
|
|
|
FI | FI | ||
|
|
|
|
|
|
FI | FI |
On a exactement le même tableau pour la limite de
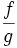
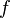
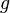
|
|
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
FI | FI |
|
|
||
|
|
|
|
FI | FI |
|
|
||
|
|
|
|
|
|
FI | FI | ||
|
|
|
|
|
|
FI | FI |
Formes indéterminées
Les formes indéterminées sont soit de type additif :
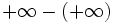
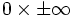

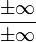
Pour parvenir à lever l'indétermination, on utilise une ou plusieurs des techniques suivantes :
- On essaye de transformer l'écriture (factorisation, développement, etc.)
- On utilise les résultats sur les croissances comparées des fonctions usuelles (voir Limites de référence)
- On applique les propriétés classiques des limites
Exemple : on cherche à calculer
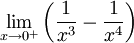
-
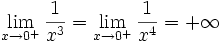
-
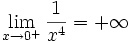
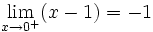
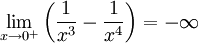
Composition
Soient :
- f une fonction définie sur J;
- g une fonction définie sur I telle que
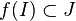
-
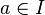
Si :
Alors