Fonction de répartition - Définition
En probabilité, la fonction de répartition d'une variable aléatoire X est la fonction 
qui à tout réel x associe
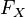
![F_X(x) = P[X\leq x].](https://static.techno-science.net/illustration/Definitions/autres/e/e3dfee626decb504a8ffc4a17d384086_3b8a0fbca7a7b6d2ce2804d6844d341a.png){kind=small}
Fonction de répartition de la loi normale centrée réduite
La fonction de répartition d'une variable aléatoire continue est la primitive de la densité de probabilité 
.
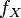
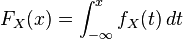
La fonction de répartition a les propriétés suivantes :
- FX est croissante.
- Elle est partout continue à droite. et admet en tout point
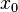
une limite à gauche, égale à ![\ P[X < x_0]](https://static.techno-science.net/illustration/Definitions/autres/e/eec5f08b038a80d891d5685086bc866b_b33b82169b97529a4bcbbe5188774d26.png)
. 
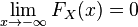
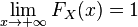
Article principal : Variable aléatoire
Populaires